| Date | May 2017 | Marks available | 5 | Reference code | 17M.3dm.hl.TZ0.2 |
| Level | HL only | Paper | Paper 3 Discrete mathematics | Time zone | TZ0 |
| Command term | Find | Question number | 2 | Adapted from | N/A |
Question
The weights of the edges in the complete graph \(G\) are given in the following table.
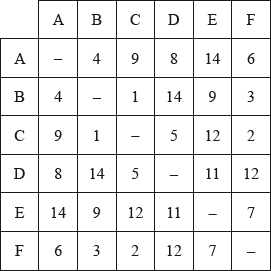
Starting at A , use the nearest neighbour algorithm to find an upper bound for the travelling salesman problem for \(G\).
By first deleting vertex A , use the deleted vertex algorithm together with Kruskal’s algorithm to find a lower bound for the travelling salesman problem for \(G\).
Markscheme
the edges are traversed in the following order
AB A1
BC
CF A1
FE
ED A1
DA A1
\({\text{upper bound}} = {\text{weight of this cycle}} = 4 + 1 + 2 + 7 + 11 + 8 = 33\) A1
[5 marks]
having deleted A, the order in which the edges are added is
BC A1
CF A1
CD A1
EF A1
Note: Accept indication of the correct order on a diagram.
to find the lower bound, we now reconnect A using the two edges with the lowest weights, that is AB and AF (M1)(A1)
\({\text{lower bound}} = 1 + 2 + 5 + 7 + 4 + 6 = 25\) A1
Note: Award (M1)(A1)A1 for \({\text{LB}} = 15 + 4 + 6 = 25\) obtained either from an incorrect order of correct edges or where order is not indicated.
[7 marks]

