| Date | November 2013 | Marks available | 3 | Reference code | 13N.3dm.hl.TZ0.4 |
| Level | HL only | Paper | Paper 3 Discrete mathematics | Time zone | TZ0 |
| Command term | Show that | Question number | 4 | Adapted from | N/A |
Question
The following diagram shows a weighted graph G with vertices A, B, C, D and E.

Show that graph \(G\) is Hamiltonian. Find the total number of Hamiltonian cycles in \(G\), giving reasons for your answer.
State an upper bound for the travelling salesman problem for graph \(G\).
Hence find a lower bound for the travelling salesman problem for \(G\).
Show that the lower bound found in (d) cannot be the length of an optimal solution for the travelling salesman problem for the graph \(G\).
Markscheme
eg the cycle \({\text{A}} \to {\text{B}} \to {\text{C}} \to {\text{D}} \to {\text{E}} \to {\text{A}}\) is Hamiltonian A1
starting from any vertex there are four choices
from the next vertex there are three choices, etc … R1
so the number of Hamiltonian cycles is \(4!{\text{ }}( = 24)\) A1
Note: Allow 12 distinct cycles (direction not considered) or 60 (if different starting points count as distinct). In any case, just award the second A1 if R1 is awarded.
[3 marks]
total weight of any Hamiltonian cycles stated
eg \({\text{A}} \to {\text{B}} \to {\text{C}} \to {\text{D}} \to {\text{E}} \to {\text{A}}\) has weight \(5 + 6 + 7 + 8 + 9 = 35\) A1
[1 mark]
a lower bound for the travelling salesman problem is then obtained by adding the weights of CA and CB to the weight of the minimum spanning tree (M1)
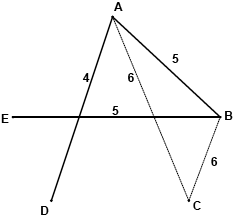
a lower bound is then \(14 + 6 + 6 = 26\) A1
[2 marks]
METHOD 1
eg eliminating A from G, a minimum spanning tree of weight 18 is (M1)
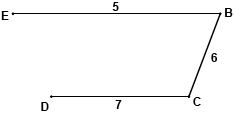
A1
adding AD and AB to the spanning tree gives a lower bound of \(18 + 4 + 5 = 27 > 26\) A1
so 26 is not the best lower bound AG
Note: Candidates may delete other vertices and the lower bounds obtained are B-28, D-27 and E-28.
METHOD 2
there are 12 distinct cycles (ignoring direction) with the following lengths
Cycle Length
ABCDEA 35 M1
ABCEDA 33
ABDCEA 39
ABDECA 37
ABECDA 31
ABEDCA 31
ACBDEA 37
ACBEDA 29
ACDBEA 35
ACEBDA 33
AEBCDA 31
AECBDA 37 A1
as the optimal solution has length 29 A1
26 is not the best possible lower bound AG
Note: Allow answers where candidates list the 24 cycles obtained by allowing both directions.
[3 marks]
Examiners report
Part (a) was generally well answered, with a variety of interpretations accepted.
Part (b) also had a number of acceptable possibilities.
Part (d) was generally well answered, but there were few good attempts at part (e).
Part (d) was generally well answered, but there were few good attempts at part (e).

