| Date | November 2017 | Marks available | 2 | Reference code | 17N.3dm.hl.TZ0.1 |
| Level | HL only | Paper | Paper 3 Discrete mathematics | Time zone | TZ0 |
| Command term | Draw | Question number | 1 | Adapted from | N/A |
Question
Mathilde delivers books to five libraries, A, B, C, D and E. She starts her deliveries at library D and travels to each of the other libraries once, before returning to library D. Mathilde wishes to keep her travelling distance to a minimum.
The weighted graph \(H\), representing the distances, measured in kilometres, between the five libraries, has the following table.
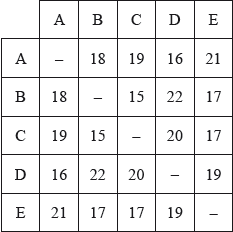
Draw the weighted graph \(H\).
Starting at library D use the nearest-neighbour algorithm, to find an upper bound for Mathilde’s minimum travelling distance. Indicate clearly the order in which the edges are selected.
By first removing library C, use the deleted vertex algorithm, to find a lower bound for Mathilde’s minimum travelling distance.
Markscheme
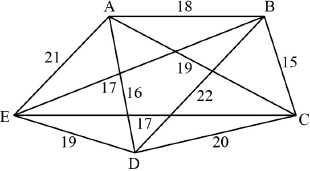
complete graph on 5 vertices A1
weights correctly marked on graph A1
[2 marks]
clear indication that the nearest-neighbour algorithm has been applied M1
DA (or 16) A1
AB (or 18) then BC (or 15) A1
CE (or 17) then ED (or 19) A1
\({\text{UB}} = 85\) A1
[5 marks]
an attempt to find the minimum spanning tree (M1)
DA (16) then BE (17) then AB (18) (total 51) A1
reconnect C with the two edges of least weight, namely CB (15) and CE (17) M1
\({\text{LB}} = 83\) A1
[4 marks]

