| Date | May 2015 | Marks available | 3 | Reference code | 15M.3dm.hl.TZ0.1 |
| Level | HL only | Paper | Paper 3 Discrete mathematics | Time zone | TZ0 |
| Command term | Calculate and Write down | Question number | 1 | Adapted from | N/A |
Question
The weights of the edges of a graph \(H\) are given in the following table.
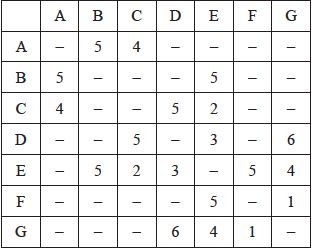
(i) Draw the weighted graph \(H\).
(ii) Use Kruskal’s algorithm to find the minimum spanning tree of \(H\). Your solution should indicate the order in which the edges are added.
(iii) State the weight of the minimum spanning tree.
Consider the following weighted graph.
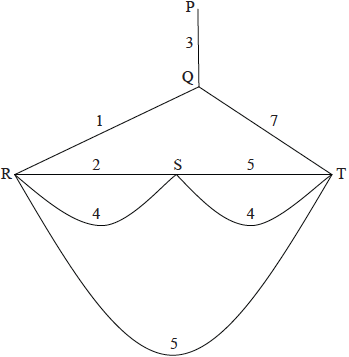
(i) Write down a solution to the Chinese postman problem for this graph.
(ii) Calculate the total weight of the solution.
(i) State the travelling salesman problem.
(ii) Explain why there is no solution to the travelling salesman problem for this graph.
Markscheme
(i) 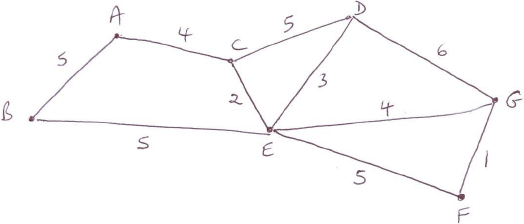 A2
A2
Note: Award A1 if one edge is missing. Award A1 if the edge weights are not labelled.
(ii) the edges are added in the order:
\(FG{\rm{ }}1\) M1A1
\(CE{\rm{ }}2\) A1
\(ED{\rm{ }}3\)
\(EG{\rm{ }}4\) A1
\(AC{\rm{ }}4\)
Note: \(EG\) and \(AC\) can be added in either order.
(Reject \(EF\))
(Reject \(CD\))
\(EB5\) OR \(AB5\) A1
Notes: The minimum spanning tree does not have to be seen.
If only a tree is seen, the order by which edges are added must be clearly indicated.
(iii) \(19\) A1
[8 marks]
(i) eg, \(PQRSRTSTQP\) OR \(PQTSTRSRQP\) M1A1
Note: Award M1 if in either (i) or (ii), it is recognised that edge \(PQ\) is needed twice.
(ii) total weight \( = 34\) A1
[3 marks]
(i) to determine a cycle where each vertex is visited once only (Hamiltonian cycle) A1
of least total weight A1
(ii) EITHER
to reach \(P\), \(Q\) must be visited twice which contradicts the definition of the \(TSP\) R1
OR
the graph is not a complete graph and hence there is no solution to the \(TSP\) R1
[3 marks]
Total [14 marks]
Examiners report
Part (a) was generally very well answered. Most candidates were able to correctly sketch the graph of \(H\) and apply Kruskal’s algorithm to determine the minimum spanning tree of \(H\). A few candidates used Prim's algorithm (which is no longer part of the syllabus).
Most candidates understood the Chinese Postman Problem in part (b) and knew to add the weight of \(PQ\) to the total weight of \(H\). Some candidates, however, did not specify a solution to the Chinese Postman Problem while other candidates missed the fact that a return to the initial vertex is required.
In part (c), many candidates had trouble succinctly stating the Travelling Salesman Problem. Many candidates used an ‘edge’ argument rather than simply stating that the Travelling Salesman Problem could not be solved because to reach vertex \(P\), vertex \(Q\) had to be visited twice.

