| Date | May 2016 | Marks available | 4 | Reference code | 16M.1.hl.TZ1.4 |
| Level | HL only | Paper | 1 | Time zone | TZ1 |
| Command term | Find | Question number | 4 | Adapted from | N/A |
Question
Two events \(A\) and \(B\) are such that \({\text{P}}(A \cap B') = 0.2\) and \({\text{P}}(A \cup B) = 0.9\).
On the Venn diagram shade the region \(A' \cap B'\).
[1]
a.
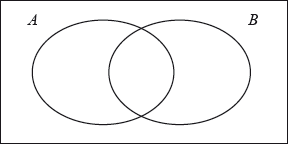
Find \({\text{P}}(A'|B')\).
[4]
b.
Markscheme
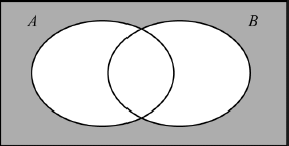A1
[1 mark]
a.
\(P(A'|B') = \frac{{P(A' \cap B')}}{{P(B')}}\) (M1)
\(P(B') = 0.1 + 0.2 = 0.3\) (A1)
\(P(A' \cap B') = 0.1\) (A1)
\(P(A'|B') = \frac{{0.1}}{{0.3}} = \frac{1}{3}\) A1
[4 marks]
b.
Examiners report
Part (a) was well done.
a.
In part (b) some candidates were unable to write down the conditional probability formula. Some then failed to realise that part (a) was designed to help them work out \(P(A' \cap B')\) and instead incorrectly assumed independence.
b.
Syllabus sections
Topic 5 - Core: Statistics and probability » 5.4 » Conditional probability; the definition \(P\left( {\left. A \right|P} \right) = \frac{{P\left( {A\mathop \cap \nolimits B} \right)}}{{P\left( B \right)}}\) .
Show 23 related questions
