| Date | May 2018 | Marks available | 1 | Reference code | 18M.2.HL.TZ2.6 |
| Level | Higher level | Paper | Paper 2 | Time zone | Time zone 2 |
| Command term | State | Question number | 6 | Adapted from | N/A |
Question
A planet has radius R. At a distance h above the surface of the planet the gravitational field strength is g and the gravitational potential is V.
State what is meant by gravitational field strength.
Show that V = –g(R + h).
Draw a graph, on the axes, to show the variation of the gravitational potential V of the planet with height h above the surface of the planet.
A planet has a radius of 3.1 × 106 m. At a point P a distance 2.4 × 107 m above the surface of the planet the gravitational field strength is 2.2 N kg–1. Calculate the gravitational potential at point P, include an appropriate unit for your answer.
The diagram shows the path of an asteroid as it moves past the planet.
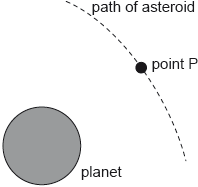
When the asteroid was far away from the planet it had negligible speed. Estimate the speed of the asteroid at point P as defined in (b).
The mass of the asteroid is 6.2 × 1012 kg. Calculate the gravitational force experienced by the planet when the asteroid is at point P.
Markscheme
the «gravitational» force per unit mass exerted on a point/small/test mass
[1 mark]
at height h potential is V = –\(\frac{{GM}}{{(R + h)}}\)
field is g = \(\frac{{GM}}{{{{(R + h)}^2}}}\)
«dividing gives answer»
Do not allow an answer that starts with g = –\(\frac{{\Delta V}}{{\Delta r}}\) and then cancels the deltas and substitutes R + h
[2 marks]
correct shape and sign
non-zero negative vertical intercept
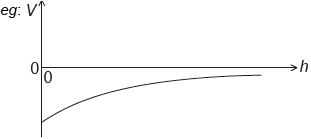
[2 marks]
V = «–2.2 × (3.1 × 106 + 2.4 × 107) =» «–» 6.0 × 107 J kg–1
Unit is essential
Allow eg MJ kg–1 if power of 10 is correct
Allow other correct SI units eg m2s–2, N m kg–1
[1 mark]
total energy at P = 0 / KE gained = GPE lost
«\(\frac{1}{2}\)mv2 + mV = 0 ⇒» v = \(\sqrt { - 2V} \)
v = «\(\sqrt {2 \times 6.0 \times {{10}^7}} \) =» 1.1 × 104 «ms–1»
Award [3] for a bald correct answer
Ignore negative sign errors in the workings
Allow ECF from 6(b)
[3 marks]
ALTERNATIVE 1
force on asteroid is «6.2 × 1012 × 2.2 =» 1.4 × 1013 «N»
«by Newton’s third law» this is also the force on the planet
ALTERNATIVE 2
mass of planet = 2.4 x 1025 «kg» «from V = –\(\frac{{GM}}{{(R + h)}}\)»
force on planet «\(\frac{{GMm}}{{{{(R + h)}^2}}}\)» = 1.4 × 1013 «N»
MP2 must be explicit
[2 marks]

