| Date | May 2018 | Marks available | 4 | Reference code | 18M.2.SL.TZ2.1 |
| Level | Standard level | Paper | Paper 2 | Time zone | Time zone 2 |
| Command term | Determine | Question number | 1 | Adapted from | N/A |
Question
A small ball of mass m is moving in a horizontal circle on the inside surface of a frictionless hemispherical bowl.
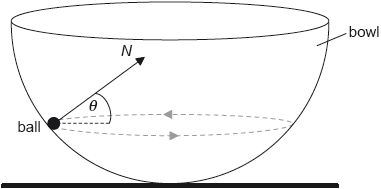
The normal reaction force N makes an angle θ to the horizontal.
State the direction of the resultant force on the ball.
On the diagram, construct an arrow of the correct length to represent the weight of the ball.
Show that the magnitude of the net force F on the ball is given by the following equation.
\[F = \frac{{mg}}{{\tan \theta }}\]
The radius of the bowl is 8.0 m and θ = 22°. Determine the speed of the ball.
Outline whether this ball can move on a horizontal circular path of radius equal to the radius of the bowl.
A second identical ball is placed at the bottom of the bowl and the first ball is displaced so that its height from the horizontal is equal to 8.0 m.
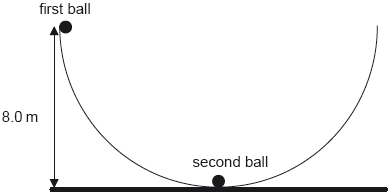
The first ball is released and eventually strikes the second ball. The two balls remain in contact. Determine, in m, the maximum height reached by the two balls.
Markscheme
towards the centre «of the circle» / horizontally to the right
Do not accept towards the centre of the bowl
[1 mark]
downward vertical arrow of any length
arrow of correct length
Judge the length of the vertical arrow by eye. The construction lines are not required. A label is not required
eg: 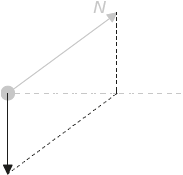
[2 marks]
ALTERNATIVE 1
F = N cos θ
mg = N sin θ
dividing/substituting to get result
ALTERNATIVE 2
right angle triangle drawn with F, N and W/mg labelled
angle correctly labelled and arrows on forces in correct directions
correct use of trigonometry leading to the required relationship
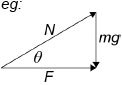
tan θ = \(\frac{{\text{O}}}{A} = \frac{{mg}}{F}\)
[3 marks]
\(\frac{{mg}}{{\tan \theta }}\) = m\(\frac{{{v^2}}}{r}\)
r = R cos θ
v = \(\sqrt {\frac{{gR{{\cos }^2}\theta }}{{\sin \theta }}} /\sqrt {\frac{{gR\cos \theta }}{{\tan \theta }}} /\sqrt {\frac{{9.81 \times 8.0\cos 22}}{{\tan 22}}} \)
v = 13.4/13 «ms –1»
Award [4] for a bald correct answer
Award [3] for an answer of 13.9/14 «ms –1». MP2 omitted
[4 marks]
there is no force to balance the weight/N is horizontal
so no / it is not possible
Must see correct justification to award MP2
[2 marks]
speed before collision v = «\(\sqrt {2gR} \) =» 12.5 «ms–1»
«from conservation of momentum» common speed after collision is \(\frac{1}{2}\) initial speed «vc = \(\frac{{12.5}}{2}\) = 6.25 ms–1»
h = «\(\frac{{{v_c}^2}}{{2g}} = \frac{{{{6.25}^2}}}{{2 \times 9.81}}\)» 2.0 «m»
Allow 12.5 from incorrect use of kinematics equations
Award [3] for a bald correct answer
Award [0] for mg(8) = 2mgh leading to h = 4 m if done in one step.
Allow ECF from MP1
Allow ECF from MP2
[3 marks]

