| Date | May 2014 | Marks available | 5 | Reference code | 14M.2.HL.TZ2.9 |
| Level | Higher level | Paper | Paper 2 | Time zone | Time zone 2 |
| Command term | Calculate and Determine | Question number | 9 | Adapted from | N/A |
Question
This question is about the thermodynamics of a car engine and the dynamics of the car.
A car engine consists of four cylinders. In each of the cylinders, a fuel-air mixture explodes to supply power at the appropriate moment in the cycle.
The diagram models the variation of pressure P with volume V for one cycle of the gas, ABCDA, in one of the cylinders of the engine. The gas in the cylinder has a fixed mass and can be assumed to be ideal.
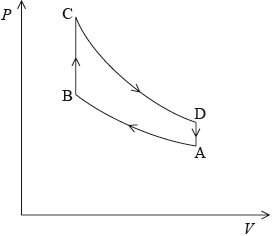
The car is travelling at its maximum speed of \({\text{56 m}}\,{{\text{s}}^{ - 1}}\). At this speed, the energy provided by the fuel injected into one cylinder in each cycle is 9200 J. One litre of fuel provides 56 MJ of energy.
A car is travelling along a straight horizontal road at its maximum speed of \({\text{56 m}}\,{{\text{s}}^{ - 1}}\). The power output required at the wheels is 0.13 MW.
A driver moves a car in a horizontal circular path of radius 200 m. Each of the four tyres will not grip the road if the frictional force between a tyre and the road becomes less than 1500 N.
At point A in the cycle, the fuel-air mixture is at 18 °C. During process AB, the gas is compressed to 0.046 of its original volume and the pressure increases by a factor of 40. Calculate the temperature of the gas at point B.
State the nature of the change in the gas that takes place during process BC in the cycle.
Process CD is an adiabatic change. Discuss, with reference to the first law of thermodynamics, the change in temperature of the gas in the cylinder during process CD.
Explain how the diagram can be used to calculate the net work done during one cycle.
(i) Calculate the volume of fuel injected into one cylinder during one cycle.
(ii) Each of the four cylinders completes a cycle 18 times every second. Calculate the distance the car can travel on one litre of fuel at a speed of \({\text{56 m}}\,{{\text{s}}^{ - 1}}\).
A car accelerates uniformly along a straight horizontal road from an initial speed of \({\text{12 m}}\,{{\text{s}}^{ - 1}}\) to a final speed of \({\text{28 m}}\,{{\text{s}}^{ - 1}}\) in a distance of 250 m. The mass of the car is 1200 kg. Determine the rate at which the engine is supplying kinetic energy to the car as it accelerates.
(i) Calculate the total resistive force acting on the car when it is travelling at a constant speed of \({\text{56 m}}\,{{\text{s}}^{ - 1}}\).
(ii) The mass of the car is 1200 kg. The resistive force F is related to the speed v by \(F \propto {v^2}\). Using your answer to (g)(i), determine the maximum theoretical acceleration of the car at a speed of \({\text{28 m}}\,{{\text{s}}^{ - 1}}\).
(i) Calculate the maximum speed of the car at which it can continue to move in the circular path. Assume that the radius of the path is the same for each tyre.
(ii) While the car is travelling around the circle, the people in the car have the sensation that they are being thrown outwards. Outline how Newton’s first law of motion accounts for this sensation.
Markscheme
535 (K) / 262 (°C);
constant volume change / isochoric / isovolumetric / OWTTE;
Q/thermal energy transfer is zero;
\(\Delta U = - W\);
as work is done by gas internal energy falls;
temperature falls as temperature is measure of average kinetic energy;
work done is estimated by evaluating area;
inside the loop / OWTTE;
(i) \(1.6 \times {10^{ - 4}}{\text{ (litre)}}\);
(ii) one litre \( = \left( {\frac{1}{{4 \times 18 \times 1.64 \times {{10}^{ - 4}}}} = } \right){\text{ }}87{\text{ s of travel}}\);
\((87 \times 56) = 4.7{\text{ (km)}}\);
Allow rounded 1.6 value to be used, giving 4.9 (km).
use of a kinematic equation to determine motion time \({\text{(}} = 12.5{\text{ s)}}\);
change in kinetic energy \( = \frac{1}{2} \times {\text{1200}} \times {\text{[2}}{{\text{8}}^2} - {\text{1}}{{\text{2}}^2}]{\text{ (}} = 384{\text{ kJ)}}\);
rate of change in kinetic energy \( = \frac{{{\text{384000}}}}{{{\text{12.5}}}}\); } (allow ECF of 162 from (28 \( - \) 12)2 for this mark)
31 (kW);
or
use of a kinematic equation to determine motion time \(( = 12.5{\text{ s)}}\);
use of a kinematic equation to determine acceleration \(( = 1.28{\text{ m}}\,{{\text{s}}^{ - 2}})\);
work done \(\frac{{F \times s}}{{{\text{time}}}} = \frac{{1536 \times 250}}{{12.5}}\);
31 (kW);
(i) \({\text{force}} = \frac{{{\text{power}}}}{{{\text{speed}}}}\);
2300 or 2.3k (N);
Award [2] for a bald correct answer.
(ii) resistive force \( = \frac{{2300}}{4}\)\(\,\,\,\)or\(\,\,\,\)\(\frac{{2321}}{4}{\text{ }}( = {\text{575)}}\); (allow ECF)
so accelerating force \((2300 - 580 = ){\text{ }}1725{\text{ (N)}}\)\(\,\,\,\)or\(\,\,\,\)1741 (N);
\(a = \frac{{1725}}{{1200}} = 1.44{\text{ (m}}\,{{\text{s}}^{ - 2}})\)\(\,\,\,\)or\(\,\,\,\)\(a = \frac{{1741}}{{1200}} = 1.45{\text{ (m}}\,{{\text{s}}^{ - 2}})\);
Award [2 max] for an answer of 0.49 (m\(\,\)s–2 (omits 2300 N).
(i) centripetal force must be \( < 6000{\text{ (N)}}\); (allow force 6000 N)
\({v^2} = F \times \frac{r}{m}\);
\(31.6{\text{ (m}}\,{{\text{s}}^{ - 1}})\);
Allow [3] for a bald correct answer.
Allow [2 max] if 4\( \times \) is omitted, giving 15.8 (m\(\,\)s–1).
(ii) statement of Newton’s first law;
(hence) without car wall/restraint/friction at seat, the people in the car would move in a straight line/at a tangent to circle;
(hence) seat/seat belt/door exerts centripetal force;
(in frame of reference of the people) straight ahead movement is interpreted as “outwards”;
Examiners report
This simple gas law calculation was surprisingly badly done. Certainly similar questions have attracted better scores in previous examinations. Common errors included the inevitable failure to work in kelvin, and simple arithmetic errors.
Most candidates were able to describe the constant volume nature of the change in question.
Many candidates scored full credit in a question that has been well rehearsed in previous examinations. The zero change in thermal energy transfer was common and many were able to deduce that \(\Delta U\) is therefore equal to \( - W\). This led immediately to a deduction of temperature decrease.
Almost all recognised that the work done was related to some area under the graph. In a small minority of cases the exact specification of the area was too imprecise to gain the second mark.
(i) It was common to see a correct value for the volume of fuel used though not a correct unit.
(ii) Many were able to arrive at a travel time for the fuel and therefore the distance travelled. However, routes were indirect and lengthy and few could see a direct way to the answer.
There were at least two routes to tackle this problem. Some solutions were so confused that it was difficult to decide which method had been used. Common errors included: forgetting that the initial speed was \({\text{12 m}}\,{{\text{s}}^{ - 1}}\) not zero, power of ten errors, and simple mistakes in the use of the kinematic equations, or failure to evaluate work done \( = {\text{force }} \times {\text{ distance}}\) correctly. However, many candidates scored partial credit. Scores of two or three out of the maximum four were common showing that many are persevering to get as far as they can.
(i) Many correct solutions were seen. Candidates are clearly comfortable with the use of the equation force = power/speed.
(ii) The method to be used here was obvious to many. What was missing was a clear appreciation of what was happening in terms of resistive force in the system. Many scored two out of three because they indicated a sensible method but did not use the correct value for the force. Scoring two marks does require that the explanation of the method is at least competent. Those candidates who give limited explanations of their method leading to a wrong answer will generally accumulate little credit. A suggestion (never seen in answers) is that candidates should have begun from a free-body force diagram which would have revealed the relationship of all the forces.
(i) The major problem here was that most candidates did not recognise that 1500 N of force acting at each of four wheels will imply a total force of 6 kN. Again, partial credit was available only if it was clear what the candidate was doing and what the error was.
(ii) Statements of Newton’s first law were surprisingly poor. As in previous examinations, few candidates appear to have learnt this essential rule by heart and they produce a garbled and incomplete version under examination pressure. The first law was then only loosely connected to the particular context of the question. Candidates have apparently not learnt to relate the physics they learn to everyday contexts.

