| Date | November 2011 | Marks available | 3 | Reference code | 11N.3.hl.TZ0.E3 |
| Level | HL | Paper | 3 | Time zone | TZ0 |
| Command term | Determine | Question number | E3 | Adapted from | N/A |
Question
Raw sewage is the water-carried waste that flows away from a community. If it is discharged untreated into rivers and the sea it causes pollution. Therefore, waste water should be treated before it is discharged.
Phosphate ions are one of the pollutants removed from sewage water by chemical precipitation using calcium ions.
The solubility product, \({K_{{\text{sp}}}}\), of calcium phosphate, \({\text{C}}{{\text{a}}_{\text{3}}}{{\text{(P}}{{\text{O}}_{\text{4}}}{\text{)}}_{\text{2}}}\), is \(1.20 \times {10^{ - 26}}\) at 298 K.
Determine the concentration of phosphate ions, in \({\text{mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\), in a saturated solution of calcium phosphate.
Markscheme
\({K_{{\text{sp}}}} = {{\text{[C}}{{\text{a}}^{2 + }}{\text{]}}^3}{{\text{[PO}}_4^{3 - }{\text{]}}^2}\);
\({\text{[C}}{{\text{a}}^{2 + }}{\text{]}} = \frac{3}{2}{\text{[PO}}_4^{3 - }{\text{]}}\) and \(1.20 \times {10^{ - 26}}{\text{ (mo}}{{\text{l}}^5}\,{\text{d}}{{\text{m}}^{ - 15}}{\text{)}} = {\left[ {\frac{3}{2}{\text{[PO}}_4^{3 - }{\text{]}}} \right]^3}{{\text{[PO}}_4^{3 - }{\text{]}}^2}\);
\({\text{[PO}}_4^{3 - }{\text{]}} = 5.13 \times {10^{ - 6}}{\text{ (mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{)}}\);
OR
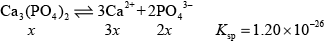
\({K_{{\text{sp}}}} = {{\text{[C}}{{\text{a}}^{2 + }}{\text{]}}^3}{{\text{[PO}}_4^{3 - }{\text{]}}^2}\);
\( = {(3x)^3}.{(2x)^2}\)
\( = 27{x^3}.4{x^2}\)
\( = 108{x^5}\)
\(\therefore x = \sqrt[5]{{\frac{{1.20 \times {{10}^{ - 26}}}}{{108}}}}\)
\( = \sqrt[5]{{1.1111 \times {{10}^{ - 28}}}}\)
\(x = 2.565 \times {10^{ - 6}}\);
\(\therefore {\text{[PO}}_4^{3 - }{\text{]}} = 2x\)
\( = 2 \times 2.565 \times {10^{ - 6}}\)
\( = 5.13 \times {10^{ - 6}}{\text{ mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\);
Award [3] for correct final answer.
Examiners report
\({K_{{\text{sp}}}}\) problem proved very difficult and was solved fully by only a few candidates. The first challenge they had was stating the \({K_{{\text{sp}}}}\) equation correctly. Half scored 1 or 2 marks through ECF, but there were enough cases where the calculation was not attempted at all. It seems processes for obtaining fresh water from sea water was not covered or covered superficially by many schools.

