| Date | May 2017 | Marks available | 1 | Reference code | 17M.1.hl.TZ0.11 |
| Level | HL only | Paper | 1 | Time zone | TZ0 |
| Command term | Verify | Question number | 11 | Adapted from | N/A |
Question
The simple connected planar graph \(J\) has the following adjacency table.
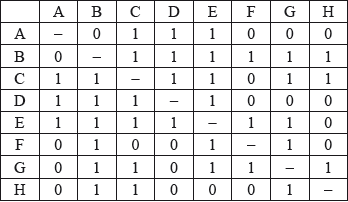
Without attempting to draw \(J\), verify that J satisfies the handshaking lemma;
Without attempting to draw \(J\), determine the number of faces in \(J\).
The vertices D and G are joined by a single edge to form the graph \(K\). Show that \(K\) is not planar.
Explain why a graph containing a cycle of length three cannot be bipartite.
Hence by finding a cycle of length three, show that the complement of \(K\) is not bipartite.
Markscheme
the sum of degrees of the vertices is even (36) or the sum of degrees of the vertices is twice the number of edges A1
[2 marks]
the number of edges \((e)\) is 18 A1
using Euler’s relation \(v - e + f = 2\) M1
\(f = 2 + 18 - 8 = 12\) A1
[2 marks]
if \(K\) is planar then \(e \leqslant 3v - 6\) M1
\(v = 8\) and \(e = 19\) A1
the inequality is not satisfied so \(K\) is not planar A1AG
[3 marks]
let PQRP be a cycle of length 3 in a graph M1
Note: Accept a diagram instead of this statement.
suppose the graph is bipartite
then P must belong to one of the two disjoint sets of vertices and Q, R must belong to the other disjoint set R1
but Q, R cannot belong to the same set because they are linked R1
therefore the graph cannot be bipartite AG
[??? marks]
for example, a suitable cycle of order 3 is AFHA (M1)A1
Note: Award M1 for a valid attempt at drawing the complement or constructing its adjacency table.
[??? marks]

