| Date | May 2010 | Marks available | 9 | Reference code | 10M.1.hl.TZ0.4 |
| Level | HL only | Paper | 1 | Time zone | TZ0 |
| Command term | Prove that | Question number | 4 | Adapted from | N/A |
Question
Given that \({n^2} + 2n + 3 \equiv N(\bmod 8)\) , where \(n \in {\mathbb{Z}^ + }\) and \(0 \le N \le 7\) , prove that \(N\) can take one of only three possible values.
Markscheme
consider the following
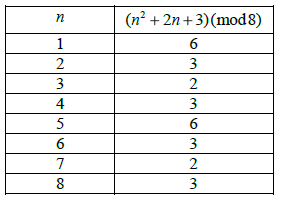 M1A1A1
M1A1A1
we see that the only possible values so far are \(2\), \(3\) and \(6\) R1
also, the table suggests that these values repeat themselves but we have to prove this
let \(f(n) = {n^2} + 2n + 3\) , consider
\(f(n + 4) - f(n) = {(n + 4)^2} + 2(n + 4) + 3 - {n^2} - 2n - 3\) M1
\( = 8n + 24\) A1
since \(8n + 24\) is divisible by \(8\), M1
\(f(n + 4) \equiv (n)(\bmod 8)\) A1
this confirms that the values do repeat every \(4\) values of \(n\) so that \(2\), \(3\) and \(6\) are the only values taken for all values of \(n\) R1
[9 marks]
Examiners report
Solutions to this question were extremely disappointing in general. Many candidates spotted that there was a periodicity in the values of the polynomial as far as \(n = 4\) and even \(n = 8\) but then the majority simply assumed that this would continue without any need for proof. This is equivalent to noting that \({2^{2n + 1}} - 1\) is prime for \(n = 1\), \(2\) and \(3\) and simply assuming that this will be true for larger values of \(n\).

