| Date | May 2008 | Marks available | 8 | Reference code | 08M.2.hl.TZ0.1 |
| Level | HL only | Paper | 2 | Time zone | TZ0 |
| Command term | Hence and Solve | Question number | 1 | Adapted from | N/A |
Question
The graph \(G\) has the following cost adjacency matrix.
Draw \(G\) in planar form.
Given that \(ax \equiv b(\bmod p)\) where \(a,b,p,x \in {\mathbb{Z}^ + }\) , \(p\) is prime and \(a\) is not a multiple of \(p\), use Fermat’s little theorem to show that
\(x \equiv {a^{p - 2}}b(\bmod p)\) .
Hence solve the simultaneous linear congruences\[3x \equiv 4(\bmod 5)\]\[5x \equiv 6(\bmod 7)\]giving your answer in the form \(x \equiv c(\bmod d)\) .
Markscheme
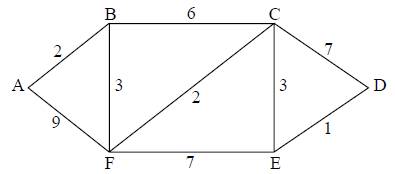
A2
[2 marks]
Note: The weights are not required for this A2.
Multiply through by \({a^{p - 2}}\) .
\({a^{p - 1}}x \equiv {a^{p - 2}}b(\bmod p)\) M1A1
Since, by Fermat’s little theorem, \({a^{p - 1}} \equiv 1(\bmod p)\) , R1
\(x \equiv {a^{p - 2}}b(\bmod p)\) AG
[3 marks]
Using the result from (a),
\(x \equiv {3^3} \times 4(\bmod 5) \equiv 3(\bmod 5)\) M1A1
\( = 3\), \(8\), \(13\), \(18\), \(23\),… (A1)
and \(x \equiv {5^5} \times 6(\bmod 7) \equiv 4(\bmod 7)\) M1A1
\( = 4\), \(11\), \(18\), \(25\),… (A1)
The general solution is
\(x = 18 + 35n\) M1
i.e. \(x \equiv 18(\bmod 35)\) A1
[8 marks]

