| Date | May 2009 | Marks available | 5 | Reference code | 09M.2.hl.TZ0.3 |
| Level | HL only | Paper | 2 | Time zone | TZ0 |
| Command term | Hence and Show that | Question number | 3 | Adapted from | N/A |
Question
Use Kruskal’s algorithm to find a minimum spanning tree for the weighted graph shown below. State the weight of the tree.
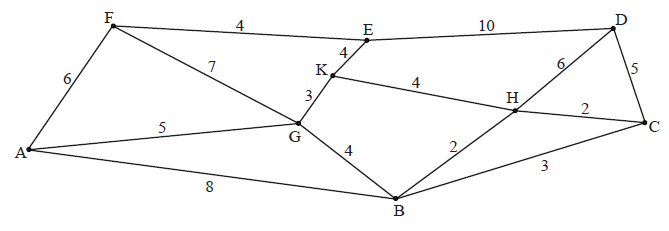
For the travelling salesman problem defined by this graph, find
(i) an upper bound;
(ii) a lower bound.
Given that the integers \(m\) and \(n\) are such that \(3|({m^2} + {n^2})\) , prove that \(3|m\) and \(3|n\) .
Hence show that \(\sqrt 2 \) is irrational.
Markscheme
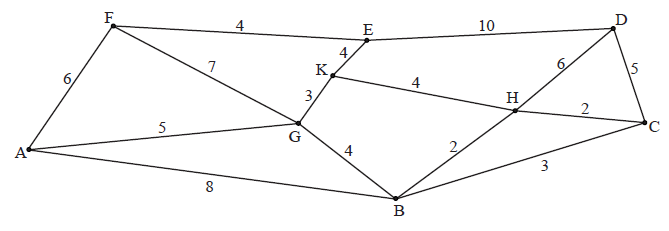
Start at an edge with weight \(2\), say BH, add other edges of weight \(2\) such that a cycle is not formed. Continue to add edges of increasing weight until all vertices have been included. M1
thus the minimum spanning tree is
\({\rm{BH + HC + GK + KH + KE + EF + GA + CD}}\) A3
total weight \( = 2 + 2 + 3 + 4 + 4 + 4 + 5 + 5 = 29\) A1
Note: GB may replace KH and other orders are possible.
[5 marks]
(i) upper bound \( = 2 \times \) weight of minimum spanning tree M1
\( = 58\) A1
(ii) deleting vertex F M1
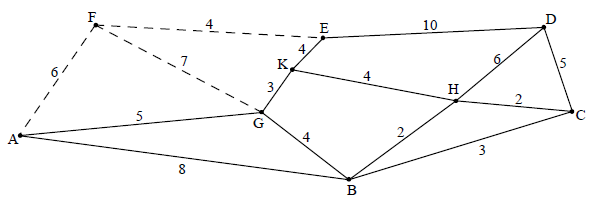
the minimum spanning tree is
\({\rm{BH + HC + GK + KE + KH + GA + CD}}\) A2
total weight \( = 2 + 2 + 3 + 4 + 4 + 5 + 5 = 25\) A1
adding the two edges of least weight from F M1
lower bound \( = 25 + 4 + 6 = 35\) A1
Note: Alternative solutions may be given by deleting a different vertex.
[8 marks]
EITHER
\(3|m \Rightarrow m \equiv 0(\bmod 3)\) (R1)
if this is false then \(m \equiv 1\) or \(2(\bmod 3)\) and \({m^2} \equiv 1\) or \(4(\bmod 3)\) R1A1
since \(4 \equiv 1(\bmod 3)\) then \({m^2} \equiv 1(\bmod 3)\) A1
similarly \({n^2} \equiv 1(\bmod 3)\) A1
hence \({m^2} + {n^2} \equiv 2(\bmod 3)\)
but \({m^2} + {n^2} \equiv 0(\bmod 3)\) (R1)
this is a contradiction so \(3|m\) and \(3|n\) R1AG
OR
\(m \equiv 0\) , 1 or \(2(\bmod 3)\) and \(n \equiv 0\) , 1 or \(2(\bmod 3)\) M1R1
\( \Rightarrow {m^2} \equiv 0\) or \(1(\bmod 3)\) and \({n^2} \equiv 0\) or \(1(\bmod 3)\) A1A1
so \({m^2} + {n^2} \equiv 0,1,2(\bmod 3)\) A1
but \(3|{m^2} + {n^2}\) so \({m^2} + {n^2} \equiv 0(\bmod 3)\) R1
\(m \equiv 0(\bmod 3)\) and \(n \equiv 0(\bmod 3)\) R1
\( \Rightarrow 3|m\) and \(3|n\) AG
[7 marks]
suppose \(\sqrt 2 = \frac{a}{b}\) , where \(a,b \in \mathbb{Z}\) and \(a\) and \(b\) are coprime M1
then
\(2{b^2} = {a^2}\) A1
\({a^2} + {b^2} = 3{b^2}\) A1
\(3{b^2} \equiv 0(\bmod 3)\) A1
but by (a) \(a\) and \(b\) have a common factor so \(\sqrt 2 \ne \frac{a}{b}\) R1
\( \Rightarrow \sqrt 2 \) is irrational AG
[5 marks]
Examiners report
This was usually well done although some candidates have difficulty showing clearly the procedure through the algorithm.
This was usually well done although some candidates have difficulty showing clearly the procedure through the algorithm.
Part (a) was not well done although there were many suspect attempts at a proof.
If part (a) was missed it should still have been possible to use the "Hence" to complete part (b). Unfortunately this did not often happen.

