| Date | November 2013 | Marks available | 2 | Reference code | 13N.1.sl.TZ0.10 |
| Level | SL only | Paper | 1 | Time zone | TZ0 |
| Command term | Solve | Question number | 10 | Adapted from | N/A |
Question
Consider the two functions, \(f\) and \(g\), where
\(f(x) = \frac{5}{{{x^2} + 1}}\)
\(g(x) = {(x - 2)^2}\)
Sketch the graphs of \(y = f(x)\) and \(y = g(x)\) on the axes below. Indicate clearly the points where each graph intersects the y-axis.
Use your graphic display calculator to solve \(f(x) = g(x)\).
Markscheme
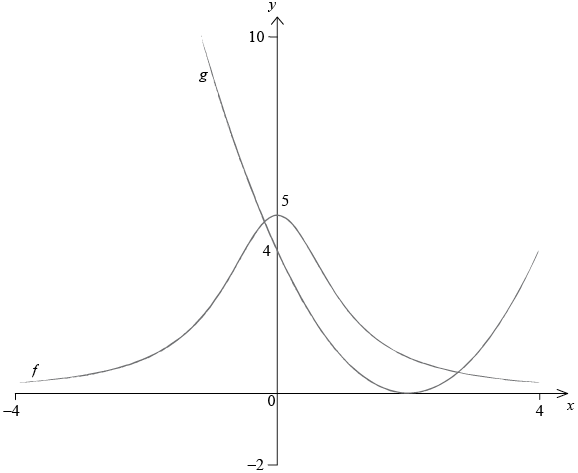
\(f(x)\): a smooth curve symmetrical about y-axis, \(f(x) > 0\) (A1)
Note: If the graph crosses the x-axis award (A0).
Intercept at their numbered \(y = 5\) (A1)
Note: Accept clear scale marks instead of a number.
\(g(x)\): a smooth parabola with axis of symmetry at about \(x = 2\) (the 2 does not need to be numbered) and \(g(x) \geqslant 0\) (A1)
Note: Right hand side must not be higher than the maximum of \(f(x)\) at \(x = 4\).
Accept the quadratic correctly drawn beyond \(x = 4\).
Intercept at their numbered \(y = 4\) (A1) (C4)
Note: Accept clear scale marks instead of a number.
[4 marks]
\(–0.195, 2.76\) \((–0.194808…, 2.761377…)\) (A1)(ft)(A1)(ft) (C2)
Note: Award (A0)(A1)(ft) if both coordinates are given.
Follow through only if \(f(x) = \frac{5}{{{x^2}}} + 1\) is sketched; the solutions are \(–0.841, 3.22\) \((–0.840913…, 3.217747...)\)
[2 marks]
Examiners report
Many candidates attempted this question but relatively few were awarded the full six marks. Although they were asked to indicate clearly where the graph met the axes, many did not do this. Some entered the functions incorrectly into their calculator. A common error in part (b) was to give ordered pairs and therefore were not awarded the final mark.
Many candidates attempted this question but relatively few were awarded the full six marks. Although they were asked to indicate clearly where the graph met the axes, many did not do this. Some entered the functions incorrectly into their calculator. A common error in part (b) was to give ordered pairs and therefore were not awarded the final mark.

