| Date | May 2017 | Marks available | 3 | Reference code | 17M.2.sl.TZ2.2 |
| Level | SL only | Paper | 2 | Time zone | TZ2 |
| Command term | Copy and complete | Question number | 2 | Adapted from | N/A |
Question
Consider these three propositions, in which x is a natural number.
\[\begin{array}{*{20}{l}} {p{\text{: }}x{\text{ is a factor of 60}}} \\ {q{\text{: }}x{\text{ is a multiple of 4}}} \\ {r{\text{: }}x{\text{ is a multiple of 5}}} \end{array}\]
Write down in symbolic form the compound proposition
“If \(x\) is a factor of 60 then \(x\) is a multiple of 5 or \(x\) is not a multiple of 4.”
Write down in words the compound proposition \(\neg r \wedge (p\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{ \vee } q)\).
Copy the following truth table and complete the last three columns.
State why the compound proposition \(\neg r \wedge (p\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{ \vee } q)\) is not a logical contradiction.
A row from the truth table from part (c) is given below.
Write down one value of \(x\) that satisfies these truth values.
Markscheme
\(p \Rightarrow (r \vee \neg q)\) (A1)(A1)(A1)
Note: Award (A1) for “\(p \Rightarrow \)”.
Award (A1) for “\(r \vee \neg q\)” or “\(r \vee q\)” (or “\(\neg q \vee r\)”or “\(q \vee r\)”)
Award (A1) for “\(\neg q\)”.
Award at most (A1)(A1)(A0) if parentheses are missing for \(r \vee \neg q\).
Award (A0)(A0)(A1) for \((p \Rightarrow r) \vee \neg q\).
[3 marks]
\(x\) is not a multiple of 5 and (\(x\)) is (either) a factor of 60 or (\(x\)) is a multiple of 4, but not both (A1)(A1)(A1)
Note: Award (A1) for “\(x\) is not a multiple of 5”, (A1) for “(\(x\)) is a factor of 60 or (\(x\)) is a multiple of 4 but not both”, (A1) for “and” in the correct position. Accept only “but not both” in the second (A1).
Award at most (A1)(A1)(A0) for using extra statements such as “If ...then”, “if and only if” etc.
[3 marks]
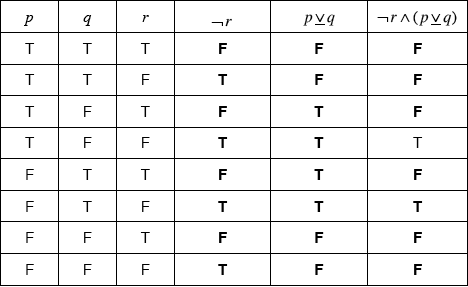(A1)(A1)(A1)(ft)
Note: Award (A1) for each correct column. Last column follows through from previous two.
[3 marks]
because not all the entries in the \(\neg r \wedge (p\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{ \vee } q)\) column are F (R1)(ft)
Note: If all entries in the last column of their truth table are T, award (R1)(ft) for an answer of “it is a tautology”. Only award (R1)(ft) if the column is identified in the justification.
[1 mark]
accept one of: 1\(\,\,\,\)OR\(\,\,\,\)2\(\,\,\,\)OR\(\,\,\,\)3\(\,\,\,\)OR\(\,\,\,\)6 (A1)
Note: Award (A1) for any one of the above answers.
[1 mark]
