| Date | November 2016 | Marks available | 1 | Reference code | 16N.1.sl.TZ0.5 |
| Level | SL only | Paper | 1 | Time zone | TZ0 |
| Command term | Determine | Question number | 5 | Adapted from | N/A |
Question
Consider the following logic propositions.
\(p\): Sandi gets up before eight o’clock
\(q\): Sandi goes for a run
\(r\): Sandi goes for a swim
Write down in words the compound proposition
Complete the following truth table.
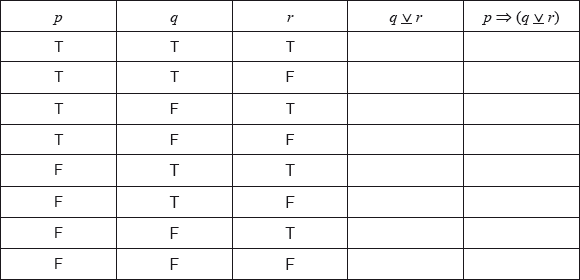
On a morning when Sandi does not get up before eight o’clock, use your truth table to determine whether \(p \Rightarrow (q{\text{ }}\underline \vee {\text{ }}r)\) is a tautology, contradiction or neither.
Markscheme
If Sandi gets up before eight o’clock then Sandi (either) goes for a run or goes for a swim, but not both. (A1)(A1)(A1) (C3)
Note: Award (A1) for If …… then ……, (A1) for all propositions in the correct order, (A1) for “… or … but not both” (do not accept “either” as a replacement for “but not both”).
[3 marks]
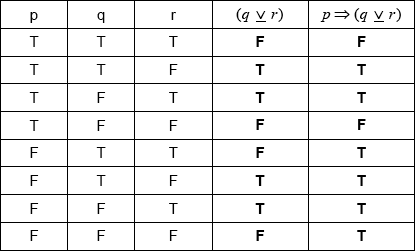(A1)(A1)(ft) (C2)
Note: Award (A1) for correct \((q{\text{ }}\underline \vee {\text{ }}r)\) column, and (A1)(ft) for their correct \(p \Rightarrow (q{\text{ }}\underline \vee {\text{ }}r)\) column. Follow through from their \((q{\text{ }}\underline \vee {\text{ }}r)\) column.
[2 marks]
tautology (A1)(ft) (C1)
Note: Follow through from part (b).
[1 mark]
