| Date | May 2013 | Marks available | 1 | Reference code | 13M.2.sl.TZ2.7 |
| Level | SL only | Paper | 2 | Time zone | TZ2 |
| Command term | Show that | Question number | 7 | Adapted from | N/A |
Question
The following diagram shows a circle with centre O and radius \(r\) cm.
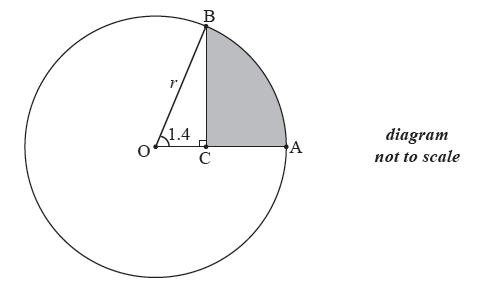
Points A and B are on the circumference of the circle and \({\rm{A}}\hat {\rm{O}}{\rm{B}} = 1.4\) radians .
The point C is on [OA] such that \({\rm{B}}\hat {\rm{C}}{\rm{O}} = \frac{\pi }{2}\) radians .
Show that \({\rm{OC}} = r\cos 1.4\) .
The area of the shaded region is \(25\) cm2 . Find the value of \(r\) .
Markscheme
use right triangle trigonometry A1
eg \(\cos 1.4 = \frac{{{\rm{OC}}}}{r}\)
\({\rm{OC}} = r\cos 1.4\) AG N0
[1 mark]
correct value for BC
eg \({\rm{BC}} = r\sin 1.4\) , \(\sqrt {{r^2} - {{(r\cos 1.4)}^2}} \) (A1)
area of \(\Delta {\rm{OBC}} = \frac{1}{2}r\sin 1.4 \times r\cos 1.4\) \(\left( { = \frac{1}{2}{r^2}\sin 1.4 \times \cos 1.4} \right)\) A1
area of sector \({{\rm{OAB}} = \frac{1}{2}{r^2} \times 1.4}\) A1
attempt to subtract in any order (M1)
eg sector – triangle, \({\frac{1}{2}{r^2}\sin 1.4 \times \cos 1.4 - 0.7{r^2}}\)
correct equation A1
eg \({0.7{r^2} - \frac{1}{2}r\sin 1.4 \times r\cos 1.4 = 25}\)
attempt to solve their equation (M1)
eg sketch, writing as quadratic, \(\frac{{25}}{{0.616 \ldots }}\)
\(r = 6.37\) A1 N4
[7 marks]
Note: Exception to FT rule. Award A1FT for a correct FT answer from a quadratic equation involving two trigonometric functions.
Examiners report
As to be expected, candidates found this problem challenging. In part (a), many were able to use right angle trigonometry to find the length of OC.
As to be expected, candidates found this problem challenging. Those who used a systematic approach in part (b) were more successful than those whose work was scattered about the page. While a pleasing number of candidates successfully found the area of sector AOB, far fewer were able to find the area of triangle BOC. Candidates who took an analytic approach to solving the resulting equation were generally less successful than those who used their GDC. Candidates who converted the angle to degrees generally were not very successful.

