| Date | May 2016 | Marks available | 3 | Reference code | 16M.2.sl.TZ2.8 |
| Level | SL only | Paper | 2 | Time zone | TZ2 |
| Command term | Estimate | Question number | 8 | Adapted from | N/A |
Question
The price of a used car depends partly on the distance it has travelled. The following table shows the distance and the price for seven cars on 1 January 2010.

The relationship between \(x\) and \(y\) can be modelled by the regression equation \(y = ax + b\).
On 1 January 2010, Lina buys a car which has travelled \(11\,000{\text{ km}}\).
The price of a car decreases by 5% each year.
Lina will sell her car when its price reaches \(10\,000\) dollars.
(i) Find the correlation coefficient.
(ii) Write down the value of \(a\) and of \(b\).
Use the regression equation to estimate the price of Lina’s car, giving your answer to the nearest 100 dollars.
Calculate the price of Lina’s car after 6 years.
Find the year when Lina sells her car.
Markscheme
Note: There may be slight differences in answers, depending on which values candidates carry through in subsequent parts. Accept answers that are consistent with their working.
(i) valid approach (M1)
eg\(\,\,\,\,\,\)correct value for \(r\) (or for \(a\) or \(b\) seen in (ii))
\( - 0.994347\)
\(r = - 0.994\) A1 N2
(ii) \( - 1.58095,{\text{ }}33480.3\)
\(a = - 1.58,{\text{ }}b = 33500\) A1A1 N2
[4 marks]
Note: There may be slight differences in answers, depending on which values candidates carry through in subsequent parts. Accept answers that are consistent with their working.
correct substitution into their regression equation
eg\(\,\,\,\,\,\)\( - 1.58095(11000){\text{ }} + 33480.3\) (A1)
\(16\,089.85{\text{ }}(16\,120{\text{ from 3sf}})\) (A1)
\({\text{price}} = 16\,100{\text{ }}({\text{dollars}})\) (must be rounded to the nearest 100 dollars) A1 N3
[3 marks]
Note: There may be slight differences in answers, depending on which values candidates carry through in subsequent parts. Accept answers that are consistent with their working.
METHOD 1
valid approach (M1)
eg\(\,\,\,\,\,\)\(P \times {({\text{rate}})^t}\)
\({\text{rate}} = 0.95\) (may be seen in their expression) (A1)
correct expression (A1)
eg\(\,\,\,\,\,\)\(16100 \times {0.95^6}\)
\(11\,834.97\)
\(11\,800{\text{ }}({\text{dollars}})\) A1 N2
METHOD 2
attempt to find all six terms (M1)
eg\(\,\,\,\,\,\)\(\left( {\left( {(16\,100 \times 0.95) \times 0.95} \right) \ldots } \right) \times 0.95\), table of values
5 correct values (accept values that round correctly to the nearest dollar)
\(15\,295,{\text{ }}14\,530,{\text{ }}13\,804,{\text{ }}13\,114,{\text{ }}12\,458\) A2
\(11\,835\)
\(11\,800{\text{ }}({\text{dollars}})\) A1 N2
[4 marks]
Note: There may be slight differences in answers, depending on which values candidates carry through in subsequent parts. Accept answers that are consistent with their working.
METHOD 1
correct equation (A1)
eg\(\,\,\,\,\,\)\(16\,100 \times {0.95^x}{\text{ = }}10\,000\)
valid attempt to solve (M1)
eg\(\,\,\,\,\,\)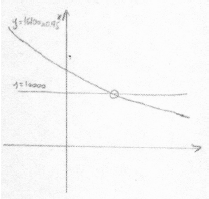 , using logs
, using logs
9.28453 (A1)
year 2019 A1 N2
METHOD 2
valid approach using table of values (M1)
both crossover values (accept values that round correctly to the nearest dollar) A2
eg\(\,\,\,\,\,\)\({\text{P}} = 10\,147{\text{ }}({\text{1 Jan 2019}}),{\text{ P}} = 9\,639.7{\text{ }}({\text{1 Jan 2020}})\)
year 2019 A1 N2
[4 marks]
Examiners report
Although the question talked about the regression equation, a few students tried to find the values of a and b by forming two equations with the coordinates of two points from the table. A considerable number of candidates did not write the value of the correlation coefficient or gave an incorrect one. It can be that a GDC feature (Diagnostics) from some calculators was turned off.
Part (b) was generally well done, with many candidates earning follow through marks. There were some difficulties in rounding the answer to the nearest 100 dollars.
Part (c) was attempted in two different ways: recognizing the correct rate 0.95 and then finding the price of the car after 6 years. Some of these candidates used a formula similar to the one for terms of a geometric sequence, \(P \times {({\text{rate)}}^{t - 1}}\), but substituted \(t\) by 6 and hence, got an incorrect result.
Others listed all six values to obtain the answer. When using this method, the problem was using less accurate intermediate results and hence, not getting the first 5 correct values of the car.
Many candidates either missed out questions 8 (c) and (d) or multiplied either \(0.05 \times 6 \times 16\,100\) or \(0.95 \times 6 \times 16\,100\) and failed to notice that the answer did not make sense. Other students tried to use the sum formula for a geometric series.
Many candidates either missed out questions 8 (c) and (d) or multiplied either \(0.05 \times 6 \times 16\,100\) or \(0.95 \times 6 \times 16\,100\) and failed to notice that the answer did not make sense. Other students tried to use the sum formula for a geometric series.
Part (d) was attempted using a graphical approach as well as analytically using logarithms to find the year in which Lina would sell the car, though many failed in giving the correct year. Common answers were “in the ninth year” or “in 2020”. The same happened to those candidates who used a table of values and found the price of the car after 9 years and 10 years. These candidates should be reminded to show both “crossover” values for a table method to be valid.

