| Date | May 2015 | Marks available | 3 | Reference code | 15M.1.sl.TZ1.9 |
| Level | SL only | Paper | 1 | Time zone | TZ1 |
| Command term | Explain | Question number | 9 | Adapted from | N/A |
Question
A function \(f\) has its derivative given by \(f'(x) = 3{x^2} - 2kx - 9\), where \(k\) is a constant.
Find \(f''(x)\).
The graph of \(f\) has a point of inflexion when \(x = 1\).
Show that \(k = 3\).
Find \(f'( - 2)\).
Find the equation of the tangent to the curve of \(f\) at \(( - 2,{\text{ }}1)\), giving your answer in the form \(y = ax + b\).
Given that \(f'( - 1) = 0\), explain why the graph of \(f\) has a local maximum when \(x = - 1\).
Markscheme
\(f''(x) = 6x - 2k\) A1A1 N2
[2 marks]
substituting \(x = 1\) into \(f''\) (M1)
eg\(\;\;\;f''(1),{\text{ }}6(1) - 2k\)
recognizing \(f''(x) = 0\;\;\;\)(seen anywhere) M1
correct equation A1
eg\(\;\;\;6 - 2k = 0\)
\(k = 3\) AG N0
[3 marks]
correct substitution into \(f'(x)\) (A1)
eg\(\;\;\;3{( - 2)^2} - 6( - 2) - 9\)
\(f'( - 2) = 15\) A1 N2
[2 marks]
recognizing gradient value (may be seen in equation) M1
eg\(\;\;\;a = 15,{\text{ }}y = 15x + b\)
attempt to substitute \(( - 2,{\text{ }}1)\) into equation of a straight line M1
eg\(\;\;\;1 = 15( - 2) + b,{\text{ }}(y - 1) = m(x + 2),{\text{ }}(y + 2) = 15(x - 1)\)
correct working (A1)
eg\(\;\;\;31 = b,{\text{ }}y = 15x + 30 + 1\)
\(y = 15x + 31\) A1 N2
[4 marks]
METHOD 1 (\({{\text{2}}^{{\text{nd}}}}\) derivative)
recognizing \(f'' < 0\;\;\;\)(seen anywhere) R1
substituting \(x = - 1\) into \(f''\) (M1)
eg\(\;\;\;f''( - 1),{\text{ }}6( - 1) - 6\)
\(f''( - 1) = - 12\) A1
therefore the graph of \(f\) has a local maximum when \(x = - 1\) AG N0
METHOD 2 (\({{\text{1}}^{{\text{st}}}}\) derivative)
recognizing change of sign of \(f'(x)\;\;\;\)(seen anywhere) R1
eg\(\;\;\;\)sign chart\(\;\;\;\)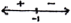
correct value of \(f'\) for \( - 1 < x < 3\) A1
eg\(\;\;\;f'(0) = - 9\)
correct value of \(f'\) for \(x\) value to the left of \( - 1\) A1
eg\(\;\;\;f'( - 2) = 15\)
therefore the graph of \(f\) has a local maximum when \(x = - 1\) AG N0
[3 marks]
Total [14 marks]
Examiners report
Well answered and candidates coped well with \(k\) in the expression.
Mostly answered well with the common error being to substitute into \(f'\) instead of \(f''\).
A straightforward question that was typically answered correctly.
Some candidates recalculated the gradient, not realising this had already been found in part c). Many understood they were finding a linear equation but were hampered by arithmetic errors.
Using change of sign of the first derivative was the most common approach used with a sign chart or written explanation. However, few candidates then supported their approach by calculating suitable values for \(f'(x)\). This was necessary because the question already identified a local maximum, hence candidates needed to explain why this was so. Some candidates did not mention the ‘first derivative’ just that ‘it’ was increasing/decreasing. Few candidates used the more efficient second derivative test.

