| Date | May 2015 | Marks available | 4 | Reference code | 15M.1.sl.TZ1.5 |
| Level | SL only | Paper | 1 | Time zone | TZ1 |
| Command term | Find | Question number | 5 | Adapted from | N/A |
Question
Given that \(\sin x = \frac{3}{4}\), where \(x\) is an obtuse angle,
find the value of \(\cos x;\)
find the value of \(\cos 2x.\)
Markscheme
valid approach (M1)
eg\(\;\;\;\)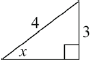 , \({\sin ^2}x + {\cos ^2}x = 1\)
, \({\sin ^2}x + {\cos ^2}x = 1\)
correct working (A1)
eg\(\;\;\;{4^2} - {3^2},{\text{ }}{\cos ^2}x = 1 - {\left( {\frac{3}{4}} \right)^2}\)
correct calculation (A1)
eg\(\;\;\;\frac{{\sqrt 7 }}{4},{\text{ }}{\cos ^2}x = \frac{7}{{16}}\)
\(\cos x = - \frac{{\sqrt 7 }}{4}\) A1 N3
[4 marks]
correct substitution (accept missing minus with cos) (A1)
eg\(\;\;\;1 - 2{\left( {\frac{3}{4}} \right)^2},{\text{ }}2{\left( { - \frac{{\sqrt 7 }}{4}} \right)^2} - 1,{\text{ }}{\left( {\frac{{\sqrt 7 }}{4}} \right)^2} - {\left( {\frac{3}{4}} \right)^2}\)
correct working A1
eg\(\;\;\;2\left( {\frac{7}{{16}}} \right) - 1,{\text{ }}1 - \frac{{18}}{{16}},{\text{ }}\frac{7}{{16}} - \frac{9}{{16}}\)
\(\cos 2x = - \frac{2}{{16}}\;\;\;\left( { = - \frac{1}{8}} \right)\) A1 N2
[3 marks]
Total [7 marks]
Examiners report
Many candidates were able to find the cosine ratio of \(\frac{{\sqrt 7 }}{4}\) but did not take into account the information about the obtuse angle and seldom selected the negative answer. Finding \(\cos 2x\) proved easier; the most common error seen was \(\cos 2x = 2\cos x\).
Many candidates were able to find the cosine ratio of \(\frac{{\sqrt 7 }}{4}\) but did not take into account the information about the obtuse angle and seldom selected the negative answer. Finding \(\cos 2x\) proved easier; the most common error seen was \(\cos 2x = 2\cos x\).

