| Date | May 2012 | Marks available | 2 | Reference code | 12M.1.sl.TZ1.7 |
| Level | SL only | Paper | 1 | Time zone | TZ1 |
| Command term | Write down | Question number | 7 | Adapted from | N/A |
Question
Let \(f(x) = {(\sin x + \cos x)^2}\) .
Show that \(f(x)\) can be expressed as \(1 + \sin 2x\) .
The graph of f is shown below for \(0 \le x \le 2\pi \) .
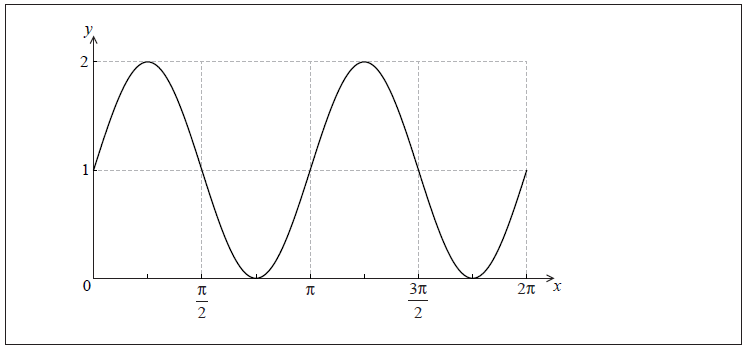
Let \(g(x) = 1 + \cos x\) . On the same set of axes, sketch the graph of g for \(0 \le x \le 2\pi \) .
The graph of g can be obtained from the graph of f under a horizontal stretch of scale factor p followed by a translation by the vector \(\left( {\begin{array}{*{20}{c}}
k\\
0
\end{array}} \right)\) .
Write down the value of p and a possible value of k .
Markscheme
attempt to expand (M1)
e.g. \((\sin x + \cos x)(\sin x + \cos x)\) ; at least 3 terms
correct expansion A1
e.g. \({\sin ^2}x + 2\sin x\cos x + {\cos ^2}x\)
\(f(x) = 1 + \sin 2x\) AG N0
[2 marks]
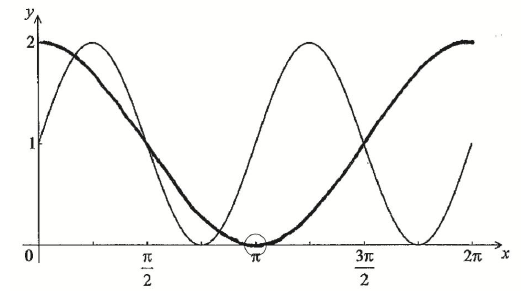 A1A1 N2
A1A1 N2
Note: Award A1 for correct sinusoidal shape with period \(2\pi \) and range \([0{\text{, }}2]\), A1 for minimum in circle.
\(p = 2\) , \(k = - \frac{\pi }{2}\) A1A1 N2
[2 marks]
Examiners report
Simplifying a trigonometric expression and applying identities was generally well answered in part (a), although some candidates were certainly helped by the fact that it was a "show that" question.
More candidates had difficulty with part (b) with many assuming the first graph was \(1 + \sin (x)\) and hence sketching a horizontal translation of \(\pi /2\) for the graph of g; some attempts were not even sinusoidal. While some candidates found the stretch factor p correctly or from follow-through on their own graph, very few successfully found the value and direction for the translation.
Part (c) certainly served as a discriminator between the grade 6 and 7 candidates.

