| Date | November 2013 | Marks available | 2 | Reference code | 13N.1.sl.TZ0.1 |
| Level | SL only | Paper | 1 | Time zone | TZ0 |
| Command term | Express | Question number | 1 | Adapted from | N/A |
Question
In the following diagram, \(\overrightarrow {{\text{OP}}} \) = p, \(\overrightarrow {{\text{OQ}}} \) = q and \(\overrightarrow {{\text{PT}}} = \frac{1}{2}\overrightarrow {{\text{PQ}}} \).
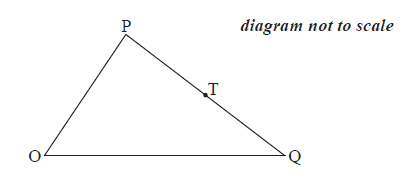
Express each of the following vectors in terms of p and q,
\(\overrightarrow {{\text{QP}}} \);
\(\overrightarrow {{\text{OT}}} \).
Markscheme
appropriate approach (M1)
eg \(\overrightarrow {{\text{QP}}} = \overrightarrow {{\text{QO}}} + \overrightarrow {{\text{OP}}} ,{\text{ P}} - {\text{Q}}\)
\(\overrightarrow {{\text{QP}}} \) = p – q A1 N2
[2 marks]
recognizing correct vector for \(\overrightarrow {{\text{QT}}} \) or \(\overrightarrow {{\text{PT}}} \) (A1)
eg \(\overrightarrow {{\text{QT}}} = \frac{1}{2}\)(p – q), \(\overrightarrow {{\text{PT}}} = \frac{1}{2}\)(q – p)
appropriate approach (M1)
eg \(\overrightarrow {{\text{OT}}} = \overrightarrow {{\text{OP}}} + \overrightarrow {{\text{PT}}} ,{\text{ }}\overrightarrow {{\text{OQ}}} + \overrightarrow {{\text{QT}}} ,{\text{ }}\overrightarrow {{\text{OP}}} + \frac{1}{2}\overrightarrow {{\text{PQ}}} \)
\(\overrightarrow {{\text{OT}}} = \frac{1}{2}\)(p + q) \(\left( {{\text{accept }}\frac{{p + q}}{2}} \right)\) A1 N2
[3 marks]

