| Date | May 2016 | Marks available | 4 | Reference code | 16M.1.sl.TZ2.9 |
| Level | SL only | Paper | 1 | Time zone | TZ2 |
| Command term | Show that | Question number | 9 | Adapted from | N/A |
Question
Fred makes an open metal container in the shape of a cuboid, as shown in the following diagram.
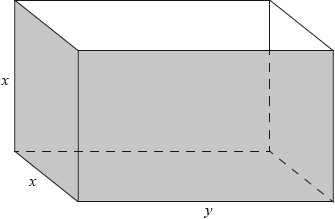
The container has height \(x{\text{ m}}\), width \(x{\text{ m}}\) and length \(y{\text{ m}}\). The volume is \(36{\text{ }}{{\text{m}}^3}\).
Let \(A(x)\) be the outside surface area of the container.
Show that \(A(x) = \frac{{108}}{x} + 2{x^2}\).
Find \(A'(x)\).
Given that the outside surface area is a minimum, find the height of the container.
Fred paints the outside of the container. A tin of paint covers a surface area of \({\text{10 }}{{\text{m}}^{\text{2}}}\) and costs $20. Find the total cost of the tins needed to paint the container.
Markscheme
correct substitution into the formula for volume A1
eg\(\,\,\,\,\,\)\(36 = y \times x \times x\)
valid approach to eliminate \(y\) (may be seen in formula/substitution) M1
eg\(\,\,\,\,\,\)\(y = \frac{{36}}{{{x^2}}},{\text{ }}xy = \frac{{36}}{x}\)
correct expression for surface area A1
eg\(\,\,\,\,\,\)\(xy + xy + xy + {x^2} + {x^2},{\text{ area}} = 3xy + 2{x^2}\)
correct expression in terms of \(x\) only A1
eg\(\,\,\,\,\,\)\(3x\left( {\frac{{36}}{{{x^2}}}} \right) + 2{x^2},{\text{ }}{x^2} + {x^2} + \frac{{36}}{x} + \frac{{36}}{x} + \frac{{36}}{x},{\text{ }}2{x^2} + 3\left( {\frac{{36}}{x}} \right)\)
\(A(x) = \frac{{108}}{x} + 2{x^2}\) AG N0
[4 marks]
\(A'(x) = - \frac{{108}}{{{x^2}}} + 4x,{\text{ }}4x - 108{x^{ - 2}}\) A1A1 N2
Note: Award A1 for each term.
[2 marks]
recognizing that minimum is when \(A'(x) = 0\) (M1)
correct equation (A1)
eg\(\,\,\,\,\,\)\( - \frac{{108}}{{{x^2}}} + 4x = 0,{\text{ }}4x = \frac{{108}}{{{x^2}}}\)
correct simplification (A1)
eg\(\,\,\,\,\,\)\( - 108 + 4{x^3} = 0,{\text{ }}4{x^3} = 108\)
correct working (A1)
eg\(\,\,\,\,\,\)\({x^3} = 27\)
\({\text{height}} = 3{\text{ (m) }}({\text{accept }}x = 3)\) A1 N2
[5 marks]
attempt to find area using their height (M1)
eg\(\,\,\,\,\,\)\(\frac{{108}}{3} + 2{(3)^2},{\text{ }}9 + 9 + 12 + 12 + 12\)
minimum surface area \( = 54{\text{ }}{{\text{m}}^{\text{2}}}\) (may be seen in part (c)) A1
attempt to find the number of tins (M1)
eg\(\,\,\,\,\,\)\(\frac{{54}}{{10}},{\text{ }}5.4\)
6 (tins) (A1)
$120 A1 N3
[5 marks]
Examiners report
Many candidates answered part (a) of this question correctly, though some seemed to be working backwards from the given expression for area, which is not the intention of a "show that" question.
In part (b), while many candidates found the correct derivative, some did so using cumbersome methods such as the quotient rule, rather than using the simpler power rule.
It was disappointing to see the number of candidates who did not recognize that the derivative they had just found in part (b) would have to be equal to zero in order for the surface area to be a minimum. For the candidates who did set their derivative equal to zero, most were able to find the correct height.
In part (d) of this question, there were some arithmetic errors which kept candidates from finding the correct area. The most common error here, by far, was not considering that the number of tins purchased must be an integer.

