
On this page we will consider the suvat equations in turn.
The suvat equations apply to uniform motion, which means constant or zero acceleration.
More complicated motion can be analysed by splitting it into steps that are so small we can assume the acceleration is constant. For example, a vehicle travelling at 10 m s-1 and then 15 m s-1 could be considered in two stages.
MY PROGRESS
How much of Equations of uniformly accelerated motion have you understood?


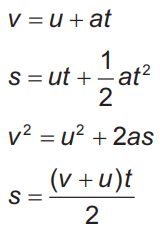
 Twitter
Twitter  Facebook
Facebook  LinkedIn
LinkedIn