Sine Rule
What is the sine rule?
- The sine rule allows us to find missing side lengths or angles in non-right-angled triangles
- It states that for any triangle with angles A, B and C
-
- Where
- a is the side opposite angle A
- b is the side opposite angle B
- c is the side opposite angle C
- Where
- This formula is in the formula booklet, you do not need to remember it
- Sin 90° = 1 so if one of the angles is 90° this becomes SOH from SOHCAHTOA

How can we use the sine rule to find missing side lengths or angles?
- The sine rule can be used when you have any opposite pairs of sides and angles
- Always start by labelling your triangle with the angles and sides
- Remember the sides with the lower-case letters are opposite the angles with the equivalent upper-case letters
- Use the formula in the formula booklet to find the length of a side
- To find a missing angle you can rearrange the formula and use the form
-
- This is not in the formula booklet but can easily be found by rearranging the one given
- Substitute the values you have into the formula and solve
Exam Tip
- Remember to check that your calculator is in degrees mode!
Worked Example
The following diagram shows triangle ABC. ,
,
.
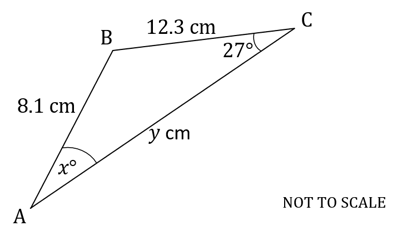
Use the sine rule to calculate the value of:
i)

ii)
Cosine Rule
What is the cosine rule?
- The cosine rule allows us to find missing side lengths or angles in non-right-angled triangles
- It states that for any triangle
;
-
- Where
- c is the side opposite angle C
- a and b are the other two sides
- Where
- Both of these formulae are in the formula booklet, you do not need to remember them
- The first version is used to find a missing side
- The second version is a rearrangement of this and can be used to find a missing angle
- Cos 90° = 0 so if C = 90° this becomes Pythagoras’ Theorem
How can we use the cosine rule to find missing side lengths or angles?
- The cosine rule can be used when you have two sides and the angle between them or all three sides
- Always start by labelling your triangle with the angles and sides
- Remember the sides with the lower-case letters are opposite the angles with the equivalent upper-case letters
- Use the formula
to find an unknown side
- Use the formula
to find an unknown angle
- C is the angle between sides a and b
- Substitute the values you have into the formula and solve
Exam Tip
- Remember to check that your calculator is in degrees mode!
Worked Example
The following diagram shows triangle .
,
,
.

Calculate the value of .

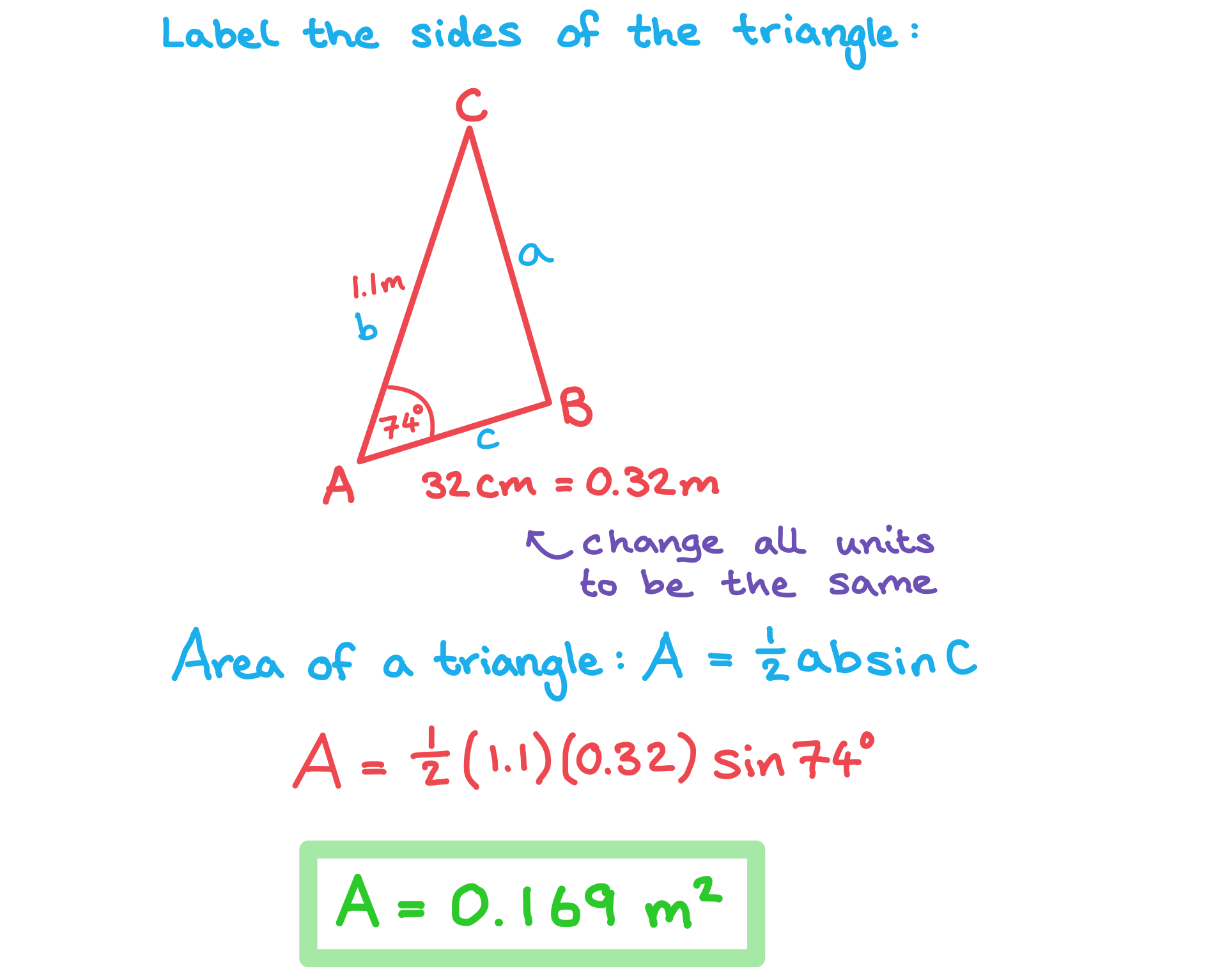
Area of a Triangle
How do I find the area of a non-right triangle?
- The area of any triangle can be found using the formula
-
- Where C is the angle between sides a and b
-
- This formula is in the formula booklet, you do not need to remember it
- Be careful to label your triangle correctly so that C is always the angle between the two sides
- Sin 90° = 1 so if C = 90° this becomes Area = ½ × base × height

Exam Tip
- Remember to check that your calculator is in degrees mode!
Worked Example
The following diagram shows triangle .
,
,
.
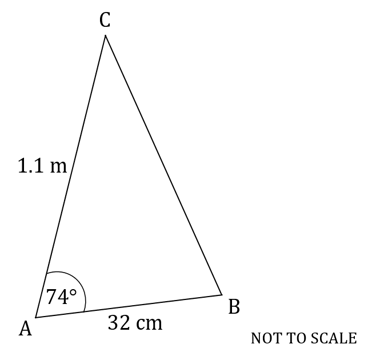
Calculate the area of triangle .