Amortisation
What is amortisation?
- Amortisation is the process of repaying a loan over a fixed period of time
- Most commonly questions will be about mortgages (loans taken out to buy a home) or loans taken out for a large purchase
- Interest will be paid on the original amount
- Each repayment that is made will partly repay the original loan and partly pay the interest on the loan
- As payments are made the amount owed will decrease and so the interest paid will decrease
- As you continue to repay a loan more of the repayment goes on the loan and less on the interest
How can the GDC be used to make calculations involving loans?
- Your GDC should be used to solve questions involving loans
- Use the finance solver mode (sometimes called the TVM (time value of money) solver)
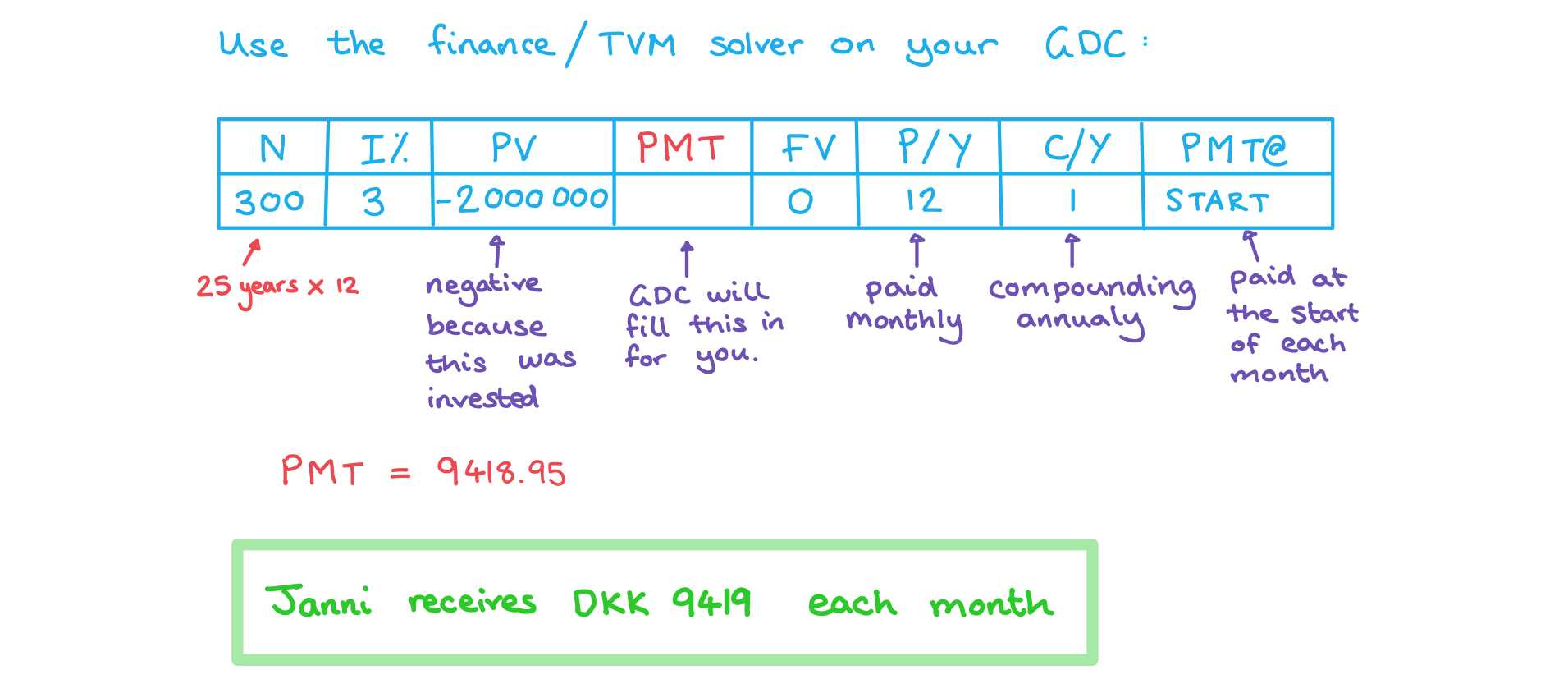
- N will be the number of repayment periods (remember to include months and years if necessary)
- I (%) is the interest rate
- PV is the amount that was borrowed at the start – as this has been received it will be entered as a positive number
- PMT is the payments made per period – this is repaying the loan so will be a negative number
- FV is the future value (this will be zero as the loan will be paid off at the end of the period)
- P/Y is the number of payments per year, usually 12 as payments are made monthly
- C/Y is the compounding periods per year
- PMT@ is the time of the year or month the payment is made (assume this is the end unless told otherwise)
- Leave the section that you need to find out blank and fill in all other sections
- Your GDC will fill in the last part for you
- Use the finance solver mode (sometimes called the TVM (time value of money) solver)
- It is sensible to check your final answer, you can do this by finding the total amount paid back overall and comparing it to the original loan
- The total amount repaid will be a little more than the original loan plus I % of the original loan
Exam Tip
- Be sure to write down the values that you put into the financial solver on your GDC, don't just write down the final answer as if it is incorrect you won't get any marks if there is no working shown!
- Make sure that you are clear on what the signage of any monetary value is, if it's positive then money is coming in to you, if it's negative then you are paying money out
Worked Example
Olivia takes a mortgage of EUR €280 000 to purchase a house at a nominal annual interest rate of 3.2%, compounded monthly. She agrees to pay the bank EUR €1500 at the end of every month to amortise the loan. Find
i)
the number of years and months it will take Olivia to pay back the loan,
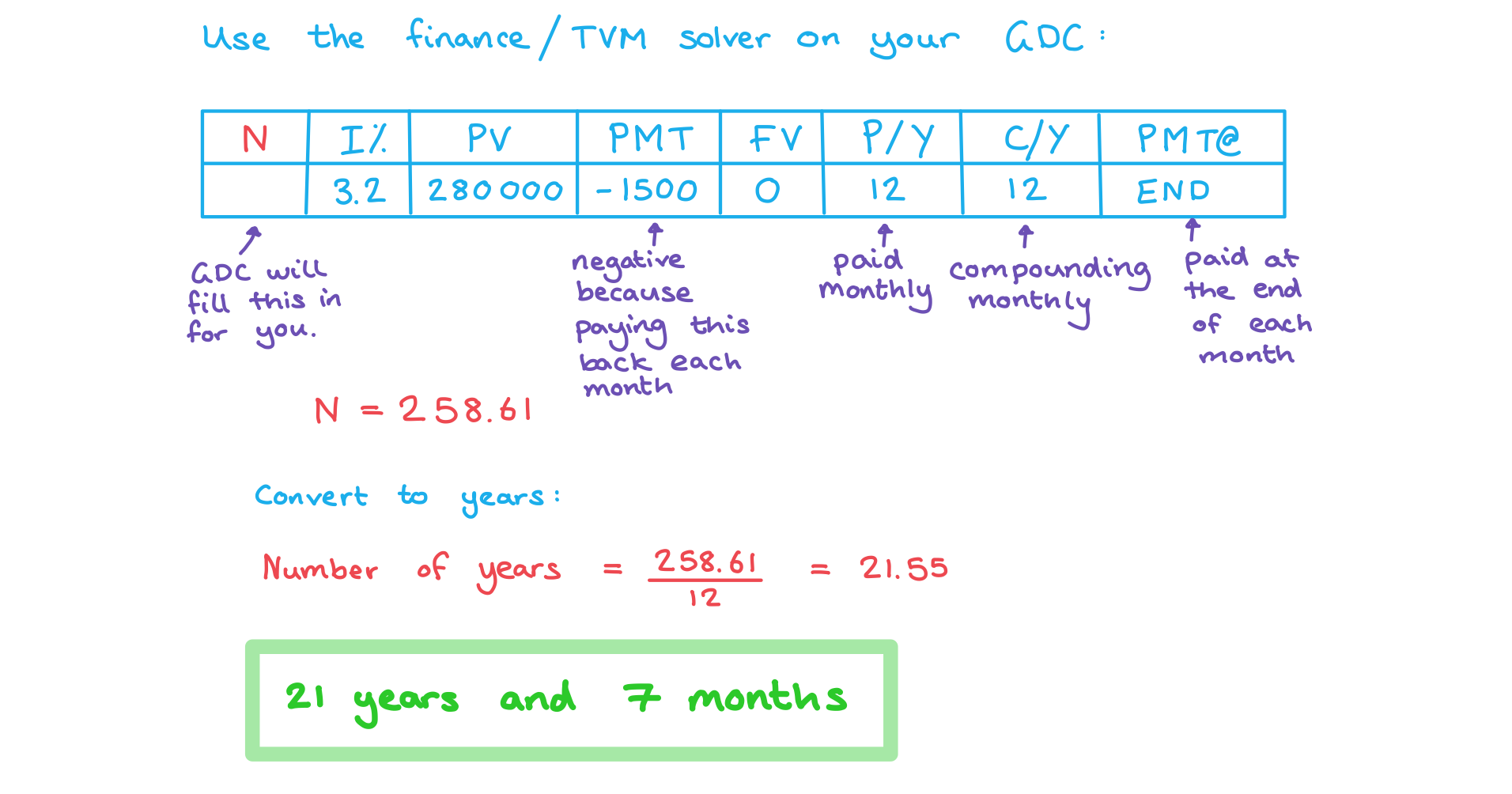
ii)
the total amount Olivia will pay to purchase the house.

Annuities
What is an annuity?
- An annuity is a fixed sum of money paid to someone at specified intervals over a fixed period of time
- Most commonly this will be because of an initial lump sum investment which will be returned at fixed intervals of time with a fixed interest rate
- Either from personal savings or from receiving an inheritance
How are annuities calculated?
- Your GDC should be used to solve questions involving annuities
- Use the finance solver mode (sometimes called the TVM (time value of money) solver)
- N will be the number of payment periods (remember to include months and years if necessary)
- I (%) is the interest rate
- PV is the amount that was invested – as this has been invested it will be entered as a negative number
- PMT is the amount paid per period – as this is being received it will be a positive number
- FV is the future value (for an annuity this will be zero as the balance at the end of the payment period will be zero)
- P/Y is the number of payments per year
- C/Y is the compounding periods per year
- PMT@ is the time of the year or month the payment is made (usually the start)
- Leave the section that you need to find out blank and fill in all other sections
- Your GDC will fill in the last part for you
- Use the finance solver mode (sometimes called the TVM (time value of money) solver)
- Although you are unlikely to need to use it, the formula for calculating an annuity is:
-
- Where
- FV is the future value
- A is the amount invested
- n is the number of years
- r% is the interest rate
- This formula is not given in the formula booklet, however your GDC will work out annuities for you so you do not need to remember it
- Where
Exam Tip
- Be sure to write down the values that you put into the financial solver on your GDC, don't just write down the final answer as if it is incorrect you won't get any marks if there is no working shown!
- Try to remember the difference between amortization and annuities:
- with amortization you are paying money out
- with annuities you are receiving money
Worked Example
Janni invests 2 million DKK (Danish krone) into an annuity for her retirement. The annuity returns 3% compounded annually. Find the monthly payments Janni will receive if she wants the annuity to last for 25 years.