2.2.3 Properties of Graphs

What are the key features of quadratic graphs?

• A quadratic graph is of the form where .
• The value of a affects the shape of the curve
  • If a is positive the shape is 
  • If a is negative the shape is 
• The y-intercept is at the point (0, c)
• The zeros or roots are the solutions to 
  • These can be found using your GDC or the quadratic formula
  • These are also called the x-intercepts
  • There can be 0, 1 or 2 x-intercepts
• There is an axis of symmetry at 
  • This is given in your formula booklet
  • If there are two x-intercepts then the axis of symmetry goes through the midpoint of them
• The vertex lies on the axis of symmetry
  • The x-coordinate is 
  • The y-coordinate can be found using the GDC or by calculating y when 
  • If a is positive then the vertex is the minimum point
  • If a is negative then the vertex is the maximum point

What are the key features of cubic graphs?

• A cubic graph is of the form  where .
• The value of a affects the shape of the curve
  • If a is positive the graph goes from bottom left to top right
  • If a is negative the graph goes from top left to bottom right
• The y-intercept is at the point (0, d)
• The zeros or roots are the solutions to 
  • These can be found using your GDC
  • These are also called the x-intercepts
  • There can be 1, 2 or 3 x-intercepts
    • There is always at least 1
• There are either 0 or 2 local minimums/maximums
  • If there are 0 then the curve is monotonic (always increasing or always decreasing)
  • If there are 2 then one is a local minimum and one is a local maximum

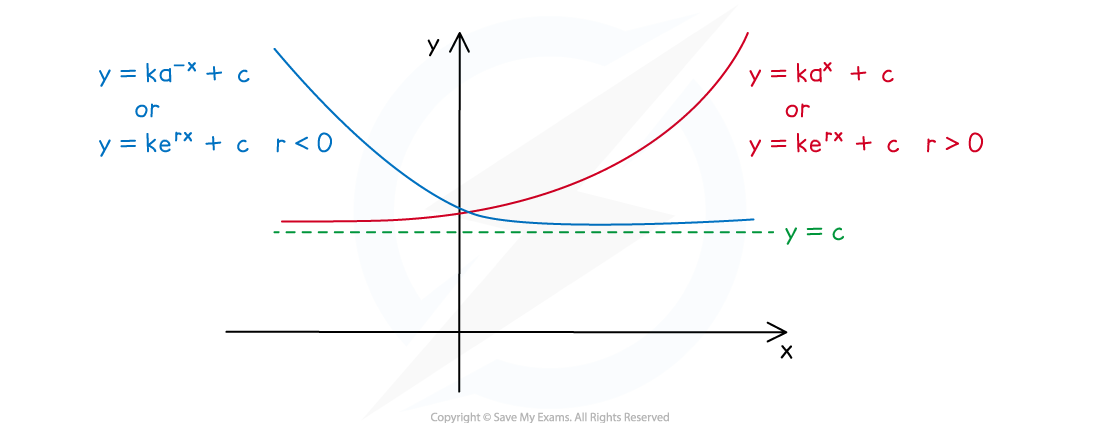
What are the key features of exponential graphs?

• An exponential graph is of the form
  • or where 
  • 
    • Where e is the mathematical constant 2.718…
• The y-intercept is at the point (0, k + c)
• There is a horizontal asymptote at y = c
• The value of k determines whether the graph is above or below the asymptote
  • If k is positive the graph is  above the asymptote
    • So the range is 
  • If k is negative the graph is below the asymptote
    • So the range is 
• The coefficient of x and the constant k determine whether the graph is increasing or decreasing
  • If the coefficient of x and k have the same sign then graph is increasing
  • If the coefficient of x and k have different signs then the graph is decreasing
• There is at most 1 root
  • It can be found using your GDC

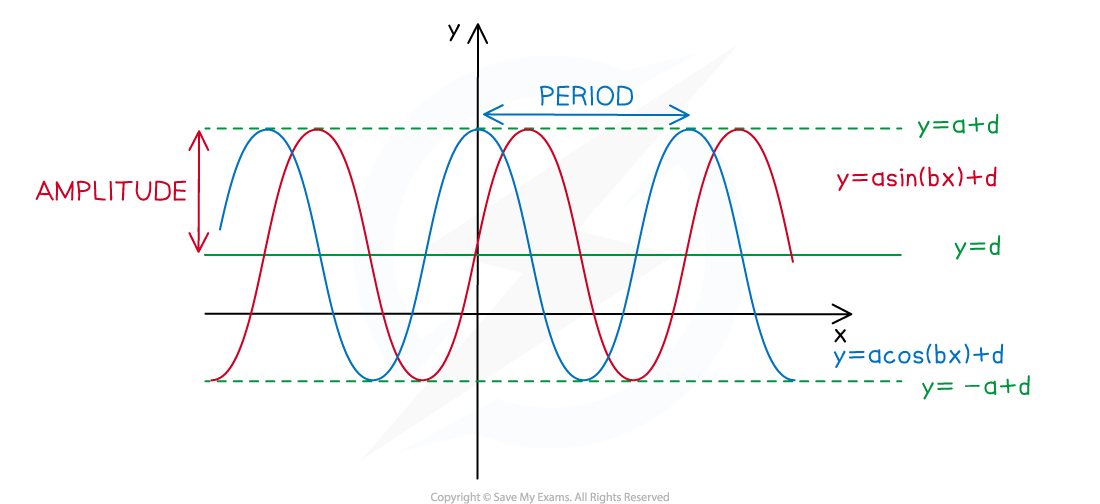
What are the key features of sinusoidal graphs?

• A sinusoidal graph is of the form
  • 
  • 
• The y-intercept is at the point
  • (0, d) for 
  • (0, a + d) for 
• The period of the graph is the length of the interval of a full cycle
  • This is 
• The maximum value is y = a + d
• The minimum value is y = -a + d
• The principal axis is the horizontal line halfway between the maximum and minimum values
  • This is y = d

• The amplitude is the vertical distance from the principal axis to the maximum value
  • This is a