| Date | November 2020 | Marks available | 1 | Reference code | 20N.2.SL.TZ0.S_7 |
| Level | Standard Level | Paper | Paper 2 | Time zone | Time zone 0 |
| Command term | Show that | Question number | S_7 | Adapted from | N/A |
Question
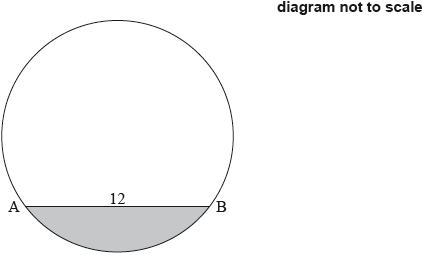
The following diagram shows a circle with centre and radius . Points and lie on the circumference of the circle and , where .
The tangents to the circle at and intersect at point .
Show that .
Find the value of when the area of the shaded region is equal to the area of sector .
Markscheme
* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.
correct working for (seen anywhere) A1
eg
AG N0
[1 mark]
METHOD 1 (working with half the areas)
area of triangle or triangle (A1)
eg
correct sector area (A1)
eg
correct approach using their areas to find the shaded area (seen anywhere) (A1)
eg
correct equation A1
eg
A2 N4
METHOD 2 (working with entire kite and entire sector)
area of kite (A1)
eg
correct sector area (A1)
eg
correct approach using their areas to find the shaded area (seen anywhere) (A1)
eg
correct equation A1
eg
A2 N4
[6 marks]