| Date | November 2016 | Marks available | 2 | Reference code | 16N.2.AHL.TZ0.H_9 |
| Level | Additional Higher Level | Paper | Paper 2 | Time zone | Time zone 0 |
| Command term | Show that | Question number | H_9 | Adapted from | N/A |
Question
The diagram shows two circles with centres at the points A and B and radii and , respectively. The point B lies on the circle with centre A. The circles intersect at the points C and D.
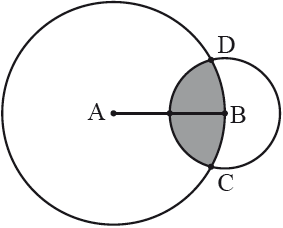
Let be the measure of the angle CAD and be the measure of the angle CBD in radians.
Find an expression for the shaded area in terms of , and .
Show that .
Hence find the value of given that the shaded area is equal to 4.
Markscheme
* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.
M1A1A1
Note: Award M1A1A1 for alternative correct expressions eg. .
[3 marks]
METHOD 1
consider for example triangle ADM where M is the midpoint of BD M1
A1
AG
METHOD 2
attempting to use the cosine rule (to obtain ) M1
(obtained from ) A1
AG
METHOD 3
where
M1
Note: Award M1 either for use of the double angle formula or the conversion from sine to cosine.
A1
AG
[2 marks]
(from triangle ADM), A1
attempting to solve
with and for (M1)
A1
[3 marks]