IB Questionbank

User interface language: English | Español

Date	November 2016	Marks available	3	Reference code	16N.2.AHL.TZ0.H_9
Level	Additional Higher Level	Paper	Paper 2	Time zone	Time zone 0
Command term	Find	Question number	H_9	Adapted from	N/A

Question

The diagram shows two circles with centres at the points A and B and radii $2r$ and $r$ , respectively. The point B lies on the circle with centre A. The circles intersect at the points C and D.

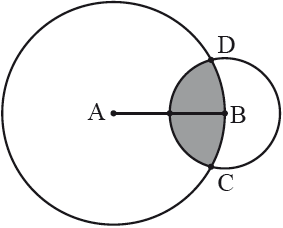
N16/5/MATHL/HP2/ENG/TZ0/09

Let $\alpha$ be the measure of the angle CAD and $\theta$ be the measure of the angle CBD in radians.

Find an expression for the shaded area in terms of $\alpha$ , $\theta$ and $r$ .

[3]

Show that $\alpha = 4\arcsin \frac{1}{4}$ .

[2]

Hence find the value of $r$ given that the shaded area is equal to 4.

[3]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

$A = 2(\alpha - \sin \alpha ){r^2} + \frac{1}{2}(\theta - \sin \theta ){r^2}$ M1A1A1

Note: Award M1A1A1 for alternative correct expressions eg. $A = 4\left( {\frac{\alpha }{2} - \sin \frac{\alpha }{2}} \right){r^2} + \frac{1}{2}\theta {r^2}$ .

[3 marks]

METHOD 1

consider for example triangle ADM where M is the midpoint of BD M1

$\sin \frac{\alpha }{4} = \frac{1}{4}$ A1

$\frac{\alpha }{4} = \arcsin \frac{1}{4}$

$\alpha = 4\arcsin \frac{1}{4}$ AG

METHOD 2

attempting to use the cosine rule (to obtain $1 - \cos \frac{\alpha }{2} = \frac{1}{8}$ ) M1

$\sin \frac{\alpha }{4} = \frac{1}{4}$ (obtained from $\sin \frac{\alpha }{4} = \sqrt {\frac{{1 - \cos \frac{\alpha }{2}}}{2}}$ ) A1

$\frac{\alpha }{4} = \arcsin \frac{1}{4}$

$\alpha = 4\arcsin \frac{1}{4}$ AG

METHOD 3

$\sin \left( {\frac{\pi }{2} - \frac{\alpha }{4}} \right) = 2\sin \frac{\alpha }{2}$ where $\frac{\theta }{2} = \frac{\pi }{2} - \frac{\alpha }{4}$

$\cos \frac{\alpha }{4} = 4\sin \frac{\alpha }{4}\cos \frac{\alpha }{4}$ M1

Note: Award M1 either for use of the double angle formula or the conversion from sine to cosine.

$\frac{1}{4} = \sin \frac{\alpha }{4}$ A1

$\frac{\alpha }{4} = \arcsin \frac{1}{4}$

$\alpha = 4\arcsin \frac{1}{4}$ AG

[2 marks]

(from triangle ADM), $\theta = \pi - \frac{\alpha }{2}{\text{ }}\left( { = \pi - 2\arcsin \frac{1}{4} = 2\arcsin \frac{1}{4} = 2.6362 \ldots } \right)$ A1

attempting to solve $2(\alpha - \sin \alpha ){r^2} + \frac{1}{2}(\theta - \sin \theta ){r^2} = 4$

with $\alpha = 4\arcsin \frac{1}{4}$ and $\theta = \pi - \frac{\alpha }{2}{\text{ }}\left( { = 2\arccos \frac{1}{4}} \right)$ for $r$ (M1)

$r = 1.69$ A1

[3 marks]

Examiners report

[N/A]

Syllabus sections

Topic 3—Geometry and trigonometry » AHL 3.7—Radians

Show 28 related questions

18N.2.AHL.TZ0.H_7:
Boat A is situated 10km away from boat B, and each boat has a marine radio transmitter on board. The range of the transmitter on boat A is 7km, and the range of the transmitter on boat B is 5km. The region in which both transmitters can be detected is represented by the shaded region in the following diagram. Find the area of this region.
16N.2.SL.TZ0.S_3a:
Write down the exact value of $\theta$ in radians.
20N.2.SL.TZ0.S_7b:
Find the value of $θ$ when the area of the shaded region is equal to the area of sector $OADB$ .
17M.2.AHL.TZ1.H_8b:
Calculate $\frac{{{\text{d}}\theta }}{{{\text{d}}t}}$ when $\theta = \frac{\pi }{3}$ .
21N.1.AHL.TZ0.15b.i:
Find an expression for $V$ in terms of $θ$ .
21N.1.AHL.TZ0.15b.ii:
Find the expression $\frac{d V}{d θ}$ .
21N.1.AHL.TZ0.15b.iii:
Solve algebraically $\frac{d V}{d θ} = 0$ to find the value of $θ$ that will maximize the volume, $V$ .
19M.1.AHL.TZ1.H_3:
A sector of a circle with radius $r$ cm , where $r$ > 0, is shown on the following diagram.
The sector has an angle of 1 radian at the centre.

Let the area of the sector be $A$ cm² and the perimeter be $P$ cm. Given that $A = P$ , find the value of $r$ .
16N.2.SL.TZ0.S_3c:
Find AB.
19M.2.SL.TZ2.S_4b:
Find the area of triangle OBC in terms of $r$ and θ.
SPM.1.AHL.TZ0.5a:
Find 50° in radians.
17M.2.SL.TZ2.S_1a:
Find the length of arc ABC.
18M.2.AHL.TZ2.H_4a.i:
Find AM.
17M.2.SL.TZ2.S_1b:
Find the perimeter of sector OABC.
17M.2.SL.TZ2.S_1c:
Find the area of sector OABC.
16N.2.AHL.TZ0.H_9c:
Hence find the value of $r$ given that the shaded area is equal to 4.
16N.2.AHL.TZ0.H_9b:
Show that $\alpha = 4\arcsin \frac{1}{4}$ .
SPM.1.AHL.TZ0.5b:
Find the volume of this log.
18M.2.AHL.TZ2.H_4b:
Find the area of the shaded region.
20N.2.SL.TZ0.S_7a:
Show that $AC = \tan θ$ .
17M.2.AHL.TZ1.H_8a:
Find an expression for the volume of water $V{\text{ }}({{\text{m}}^3})$ in the trough in terms of $\theta$ .
16N.2.AHL.TZ0.H_7a:
Use the cosine rule to find the two possible values for AC.
16N.2.AHL.TZ0.H_7b:
Find the difference between the areas of the two possible triangles ABC.
16N.2.SL.TZ0.S_3b:
Find the value of $r$ .
17N.1.SL.TZ0.S_4a:
Show that ${\text{AC}} = 7{\text{ cm}}$ .
17M.2.SL.TZ1.S_5:
The following diagram shows the chord [AB] in a circle of radius 8 cm, where ${\text{AB}} = 12{\text{ cm}}$ .

Find the area of the shaded segment.
17N.1.SL.TZ0.S_4b:
The shape in the following diagram is formed by adding a semicircle with diameter [AC] to the triangle.

Find the exact perimeter of this shape.
21N.1.AHL.TZ0.15a:
Show that $r = \frac{6}{2 + θ}$ .

Hide related questions

Topic 3—Geometry and trigonometry

Question

Markscheme

Examiners report

Syllabus sections

View options