| Date | November 2020 | Marks available | 2 | Reference code | 20N.2.HL.TZ0.9 |
| Level | Higher level | Paper | Paper 2 | Time zone | 0 - no time zone |
| Command term | Calculate | Question number | 9 | Adapted from | N/A |
Question
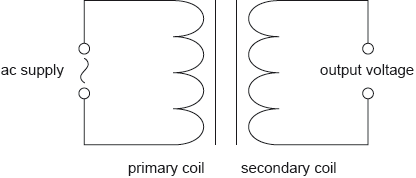
The diagram shows an alternating current generator with a rectangular coil rotating at a constant frequency in a uniform magnetic field.
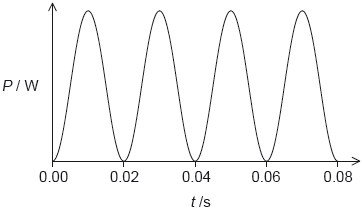
The graph shows how the generator output voltage varies with time .
Electrical power produced by the generator is delivered to a consumer some distance away.
Explain, by reference to Faraday’s law of induction, how an electromotive force (emf) is induced in the coil.
The average power output of the generator is . Calculate the root mean square (rms) value of the generator output current.
The voltage output from the generator is stepped up before transmission to the consumer. Estimate the factor by which voltage has to be stepped up in order to reduce power loss in the transmission line by a factor of .
The frequency of the generator is doubled with no other changes being made. Draw, on the axes, the variation with time of the voltage output of the generator.
Markscheme
there is a magnetic flux «linkage» in the coil / coil cuts magnetic field ✓
this flux «linkage» changes as the angle varies/coil rotates ✓
«Faraday’s law» connects induced emf with rate of change of flux «linkage» with time ✓
Do not award MP2 or 3 for answers that don’t discuss flux.
✓
✓
«power loss proportional to hence the step-up factor is ✓
peak emf doubles ✓
halves ✓
Must show at least 1 cycle.
Examiners report
This question was well answered with the majority discussing changes in flux rather than wires cutting field lines, which was good to see.
Generally well answered.
This was well answered by many, but some candidates left the answer as a surd. The most common guess here involved the use of root 2.
Well answered, with the majority of candidates scoring at least 1 mark.