ibo.org
Updates to Questionbank

User interface language: English | Español

« Back to questions in DP Physics

Date May 2019 Marks available 2 Reference code 19M.3.SL.TZ2.1
Level Standard level Paper Paper 3 Time zone 2
Command term Outline Question number 1 Adapted from N/A

Question

A student investigates the electromotive force (emf) ε and internal resistance r of a cell.

The current I and the terminal potential difference V are measured.

For this circuit V = ε - Ir .

The table shows the data collected by the student. The uncertainties for each measurement
are shown.

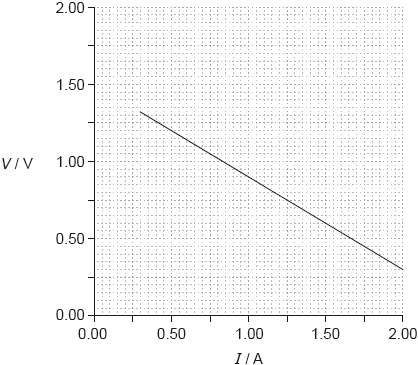
The graph shows the data plotted.

The student has plotted error bars for the potential difference. Outline why no error bars are shown for the current.

[1]
a.

Determine, using the graph, the emf of the cell including the uncertainty for this value. Give your answer to the correct number of significant figures.

[3]
b.

Outline, without calculation, how the internal resistance can be determined from this graph.

[2]
c.

Markscheme

ΔI is too small to be shown/seen

OR

Error bar of negligible size compared to error bar in V ✔

a.

evidence that ε can be determined from the y-intercept of the line of best-fit or lines of min and max gradient ✔

states ε=1.59 OR 1.60 OR 1.61V«» ✔

states uncertainty in ε is 0.02 V«» OR 0.03«V» ✔

b.

determine the gradient «of the line of best-fit» ✔

r is the negative of this gradient ✔

c.

Examiners report

Almost all candidates realised that the uncertainty in I was too small to be shown. A common mistake was to mention that since I is the independent variable the uncertainty is negligible.

a.

The number of candidates who realised that the V intercept was EMF was disappointing. Large numbers of candidates tried to calculate ε using points on the graph, often ending up with unrealistic values. Another common mistake was not giving values of ε and Δε to the correct number of digits - 2 decimal places on this occasion. Very few candidates drew maximum and minimum gradient lines as a way of determining Δε.

b.
[N/A]
c.

Syllabus sections

Core » Topic 5: Electricity and magnetism » 5.3 – Electric cells
Show 30 related questions
Hide related questions
Core » Topic 5: Electricity and magnetism
Core

View options

© International Baccalaureate Organization 2023
International Baccalaureate® - Baccalauréat International® - Bachillerato Internacional®
Terms and conditions | Privacy policy