| Date | May 2018 | Marks available | 2 | Reference code | 18M.2.HL.TZ2.4 |
| Level | Higher level | Paper | Paper 2 | Time zone | 2 |
| Command term | State | Question number | 4 | Adapted from | N/A |
Question
The diagram shows a potential divider circuit used to measure the emf E of a cell X. Both cells have negligible internal resistance.
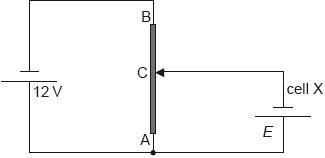
AB is a wire of uniform cross-section and length 1.0 m. The resistance of wire AB is 80 Ω. When the length of AC is 0.35 m the current in cell X is zero.
State what is meant by the emf of a cell.
Show that the resistance of the wire AC is 28 Ω.
Determine E.
Cell X is replaced by a second cell of identical emf E but with internal resistance 2.0 Ω. Comment on the length of AC for which the current in the second cell is zero.
Markscheme
the work done per unit charge
in moving charge from one terminal of a cell to the other / all the way round the circuit
Award [1] for “energy per unit charge provided by the cell”/“power per unit current”
Award [1] for “potential difference across the terminals of the cell when no current is flowing”
Do not accept “potential difference across terminals of cell”
[2 marks]
the resistance is proportional to length / see 0.35 AND 1«.00»
so it equals 0.35 × 80
«= 28 Ω»
[2 marks]
current leaving 12 V cell is = 0.15 «A»
OR
E = × 28
E = «0.15 × 28 =» 4.2 «V»
Award [2] for a bald correct answer
Allow a 1sf answer of 4 if it comes from a calculation.
Do not allow a bald answer of 4 «V»
Allow ECF from incorrect current
[2 marks]
since the current in the cell is still zero there is no potential drop across the internal resistance
and so the length would be the same
OWTTE
[2 marks]