| Date | November 2017 | Marks available | 2 | Reference code | 17N.2.hl.TZ0.10 |
| Level | HL only | Paper | 2 | Time zone | TZ0 |
| Command term | Determine | Question number | 10 | Adapted from | N/A |
Question
Consider the function \(f(x) = \frac{{\sqrt x }}{{\sin x}},{\text{ }}0 < x < \pi \).
Consider the region bounded by the curve \(y = f(x)\), the \(x\)-axis and the lines \(x = \frac{\pi }{6},{\text{ }}x = \frac{\pi }{3}\).
Show that the \(x\)-coordinate of the minimum point on the curve \(y = f(x)\) satisfies the equation \(\tan x = 2x\).
Determine the values of \(x\) for which \(f(x)\) is a decreasing function.
Sketch the graph of \(y = f(x)\) showing clearly the minimum point and any asymptotic behaviour.
Find the coordinates of the point on the graph of \(f\) where the normal to the graph is parallel to the line \(y = - x\).
This region is now rotated through \(2\pi \) radians about the \(x\)-axis. Find the volume of revolution.
Markscheme
attempt to use quotient rule or product rule M1
\(f’(x) = \frac{{\sin x\left( {\frac{1}{2}{x^{ - \frac{1}{2}}}} \right) - \sqrt x \cos x}}{{{{\sin }^2}x}}{\text{ }}\left( { = \frac{1}{{2\sqrt x \sin x}} - \frac{{\sqrt x \cos x}}{{{{\sin }^2}x}}} \right)\) A1A1
Note: Award A1 for \(\frac{1}{{2\sqrt x \sin x}}\) or equivalent and A1 for \( - \frac{{\sqrt x \cos x}}{{{{\sin }^2}x}}\) or equivalent.
setting \(f’(x) = 0\) M1
\(\frac{{\sin x}}{{2\sqrt x }} - \sqrt x \cos x = 0\)
\(\frac{{\sin x}}{{2\sqrt x }} = \sqrt x \cos x\) or equivalent A1
\(\tan x = 2x\) AG
[5 marks]
\(x = 1.17\)
\(0 < x \leqslant 1.17\) A1A1
Note: Award A1 for \(0 < x\) and A1 for \(x \leqslant 1.17\). Accept \(x < 1.17\).
[2 marks]
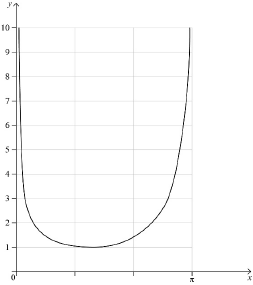
concave up curve over correct domain with one minimum point above the \(x\)-axis. A1
approaches \(x = 0\) asymptotically A1
approaches \(x = \pi \) asymptotically A1
Note: For the final A1 an asymptote must be seen, and \(\pi \) must be seen on the \(x\)-axis or in an equation.
[3 marks]
\(f’(x){\text{ }}\left( { = \frac{{\sin x\left( {\frac{1}{2}{x^{ - \frac{1}{2}}}} \right) - \sqrt x \cos x}}{{{{\sin }^2}x}}} \right) = 1\) (A1)
attempt to solve for \(x\) (M1)
\(x = 1.96\) A1
\(y = f(1.96 \ldots )\)
\( = 1.51\) A1
[4 marks]
\(V = \pi \int_{\frac{\pi }{6}}^{\frac{\pi }{3}} {\frac{{x{\text{d}}x}}{{{{\sin }^2}x}}} \) (M1)(A1)
Note: M1 is for an integral of the correct squared function (with or without limits and/or \(\pi \)).
\( = 2.68{\text{ }}( = 0.852\pi )\) A1
[3 marks]

