| Date | May 2017 | Marks available | 4 | Reference code | 17M.3dm.hl.TZ0.3 |
| Level | HL only | Paper | Paper 3 Discrete mathematics | Time zone | TZ0 |
| Command term | Find and Draw | Question number | 3 | Adapted from | N/A |
Question
In the context of graph theory, explain briefly what is meant by a circuit;
In the context of graph theory, explain briefly what is meant by an Eulerian circuit.
The graph \(G\) has six vertices and an Eulerian circuit. Determine whether or not its complement \(G'\) can have an Eulerian circuit.
Find an example of a graph \(H\), with five vertices, such that \(H\) and its complement \(H'\) both have an Eulerian trail but neither has an Eulerian circuit. Draw \(H\) and \(H'\) as your solution.
Markscheme
a circuit is a walk that begins and ends at the same vertex and has no repeated edges A1
[1 mark]
an Eulerian circuit is a circuit that contains every edge of a graph A1
[1 mark]
if \(G\) has an Eulerian circuit all vertices are even (are of degree 2 or 4) A1
hence, \(G'\) must have all vertices odd (of degree 1 or 3) R1
hence, \(G'\) cannot have an Eulerian circuit R1
Note: Award A1 to candidates who begin by considering a specific \(G\) and \(G'\) (diagram). Award R1R1 to candidates who then consider a general \(G\) and \(G'\).
[3 marks]
for example
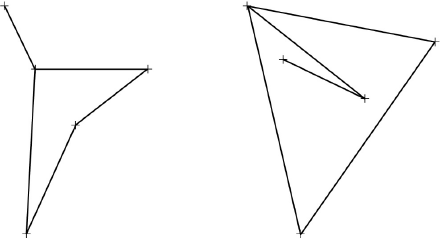
A2
A2
Notes: Each graph must have 3 vertices of order 2 and 2 odd vertices. Award A2 if one of the graphs satisfies that and the final A2 if the other graph is its complement.
[4 marks]

