| Date | May 2017 | Marks available | 3 | Reference code | 17M.2.hl.TZ2.11 |
| Level | HL only | Paper | 2 | Time zone | TZ2 |
| Command term | State | Question number | 11 | Adapted from | N/A |
Question
It is given that \(f(x) = 3{x^4} + a{x^3} + b{x^2} - 7x - 4\) where \(a\) and \(b\) are positive integers.
Given that \({x^2} - 1\) is a factor of \(f(x)\) find the value of \(a\) and the value of \(b\).
Factorize \(f(x)\) into a product of linear factors.
Sketch the graph of \(y = f(x)\), labelling the maximum and minimum points and the \(x\) and \(y\) intercepts.
Using your graph state the range of values of \(c\) for which \(f(x) = c\) has exactly two distinct real roots.
Markscheme
\(g(x) = 3{x^4} + a{x^3} + b{x^2} - 7x - 4\)
\(g(1) = 0 \Rightarrow a + b = 8\) M1A1
\(g( - 1) = 0 \Rightarrow - a + b = - 6\) A1
\( \Rightarrow a = 7,{\text{ }}b = 1\) A1
[4 marks]
\(3{x^4} + 7{x^3} + {x^2} - 7x - 4 = ({x^2} - 1)(p{x^2} + qx + r)\)
attempt to equate coefficients (M1)
\(p = 3,{\text{ }}q = 7,{\text{ }}r = 4\) (A1)
\(3{x^4} + 7{x^3} + {x^2} - 7x - 4 = ({x^2} - 1)(3{x^2} + 7x + 4)\)
\( = (x - 1){(x + 1)^2}(3x + 4)\) A1
Note: Accept any equivalent valid method.
[3 marks]
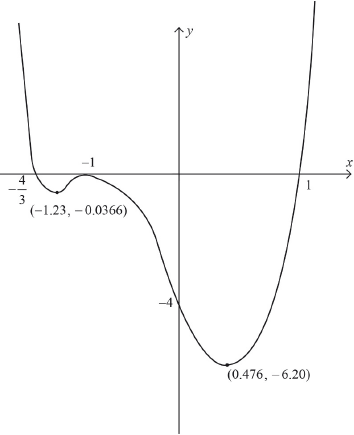
A1 for correct shape (ie with correct number of max/min points)
A1 for correct \(x\) and \(y\) intercepts
A1 for correct maximum and minimum points
[3 marks]
\(c > 0\) A1
\( - 6.20 < c < - 0.0366\) A1A1
Note: Award A1 for correct end points and A1 for correct inequalities.
Note: If the candidate has misdrawn the graph and omitted the first minimum point, the maximum mark that may be awarded is A1FTA0A0 for \(c > - 6.20\) seen.
[3 marks]

