| Date | November 2016 | Marks available | 13 | Reference code | 16N.3srg.hl.TZ0.2 |
| Level | HL only | Paper | Paper 3 Sets, relations and groups | Time zone | TZ0 |
| Command term | Find, Give a reason, Show that, and Sketch | Question number | 2 | Adapted from | N/A |
Question
Let \(A\) be the set \(\{ x|x \in \mathbb{R},{\text{ }}x \ne 0\} \). Let \(B\) be the set \(\{ x|x \in ] - 1,{\text{ }} + 1[,{\text{ }}x \ne 0\} \).
A function \(f:A \to B\) is defined by \(f(x) = \frac{2}{\pi }\arctan (x)\).
Let \(D\) be the set \(\{ x|x \in \mathbb{R},{\text{ }}x > 0\} \).
A function \(g:\mathbb{R} \to D\) is defined by \(g(x) = {{\text{e}}^x}\).
(i) Sketch the graph of \(y = f(x)\) and hence justify whether or not \(f\) is a bijection.
(ii) Show that \(A\) is a group under the binary operation of multiplication.
(iii) Give a reason why \(B\) is not a group under the binary operation of multiplication.
(iv) Find an example to show that \(f(a \times b) = f(a) \times f(b)\) is not satisfied for all \(a,{\text{ }}b \in A\).
(i) Sketch the graph of \(y = g(x)\) and hence justify whether or not \(g\) is a bijection.
(ii) Show that \(g(a + b) = g(a) \times g(b)\) for all \(a,{\text{ }}b \in \mathbb{R}\).
(iii) Given that \(\{ \mathbb{R},{\text{ }} + \} \) and \(\{ D,{\text{ }} \times \} \) are both groups, explain whether or not they are isomorphic.
Markscheme
(i) 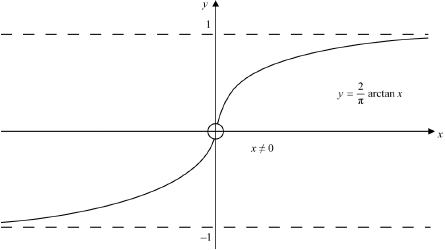 A1
A1
Notes: Award A1 for general shape, labelled asymptotes, and showing that \(x \ne 0\).
graph shows that it is injective since it is increasing or by the horizontal line test R1
graph shows that it is surjective by the horizontal line test R1
Note: Allow any convincing reasoning.
so \(f\) is a bijection A1
(ii) closed since non-zero real times non-zero real equals non-zero real A1R1
we know multiplication is associative R1
identity is 1 A1
inverse of \(x\) is \(\frac{1}{x}(x \ne 0)\) A1
hence it is a group AG
(iii) \(B\) does not have an identity A2
hence it is not a group AG
(iv) \(f(1 \times 1) = f(1) = \frac{1}{2}\) whereas \(f(1) \times f(1) = \frac{1}{2} \times \frac{1}{2} = \frac{1}{4}\) is one counterexample A2
hence statement is not satisfied AG
[13 marks]
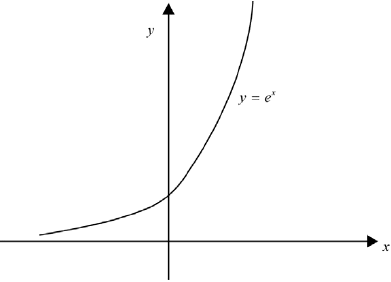
award A1 for general shape going through (0, 1) and with domain \(\mathbb{R}\) A1
graph shows that it is injective since it is increasing or by the horizontal line test and graph shows that it is surjective by the horizontal line test R1
Note: Allow any convincing reasoning.
so \(g\) is a bijection A1
(ii) \(g(a + b) = {{\text{e}}^{a + b}}\) and \(g(a) \times g(b) = {{\text{e}}^a} \times {{\text{e}}^b} = {{\text{e}}^{a + b}}\) M1A1
hence \(g(a + b) = g(a) \times g(b)\) AG
(iii) since \(g\) is a bijection and the homomorphism rule is obeyed R1R1
the two groups are isomorphic A1
[8 marks]

