| Date | November 2016 | Marks available | 2 | Reference code | 16N.3srg.hl.TZ0.1 |
| Level | HL only | Paper | Paper 3 Sets, relations and groups | Time zone | TZ0 |
| Command term | Write | Question number | 1 | Adapted from | N/A |
Question
Let \(\{ G,{\text{ }} \circ \} \) be the group of all permutations of \(1,{\text{ }}2,{\text{ }}3,{\text{ }}4,{\text{ }}5,{\text{ }}6\) under the operation of composition of permutations.
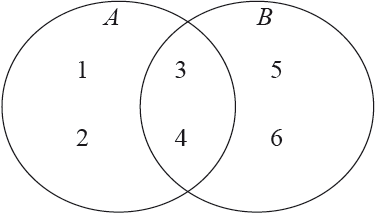
Consider the following Venn diagram, where \(A = \{ 1,{\text{ }}2,{\text{ }}3,{\text{ }}4\} ,{\text{ }}B = \{ 3,{\text{ }}4,{\text{ }}5,{\text{ }}6\} \).
(i) Write the permutation \(\alpha = \left( {\begin{array}{*{20}{c}} 1&2&3&4&5&6 \\ 3&4&6&2&1&5 \end{array}} \right)\) as a composition of disjoint cycles.
(ii) State the order of \(\alpha \).
(i) Write the permutation \(\beta = \left( {\begin{array}{*{20}{c}} 1&2&3&4&5&6 \\ 6&4&3&5&1&2 \end{array}} \right)\) as a composition of disjoint cycles.
(ii) State the order of \(\beta \).
Write the permutation \(\alpha \circ \beta \) as a composition of disjoint cycles.
Write the permutation \(\beta \circ \alpha \) as a composition of disjoint cycles.
State the order of \(\{ G,{\text{ }} \circ \} \).
Find the number of permutations in \(\{ G,{\text{ }} \circ \} \) which will result in \(A\), \(B\) and \(A \cap B\) remaining unchanged.
Markscheme
(i) \((1{\text{ }}3{\text{ }}6{\text{ }}5)(2{\text{ }}4)\) A1A1
(ii) 4 A1
Note: In (b) (c) and (d) single cycles can be omitted.
[3 marks]
(i) \((1{\text{ }}6{\text{ }}2{\text{ }}4{\text{ }}5)(3)\) A1
(ii) 5 A1
[2 marks]
\(\left( {\begin{array}{*{20}{c}} 1&2&3&4&5&6 \\ 5&2&6&1&3&4 \end{array}} \right) = (1{\text{ }}5{\text{ }}3{\text{ }}6{\text{ }}4)(2)\) (M1)A1
[2 marks]
\(\left( {\begin{array}{*{20}{c}} 1&2&3&4&5&6 \\ 3&5&2&4&6&1 \end{array}} \right) = (1{\text{ }}3{\text{ }}2{\text{ }}5{\text{ }}6)(4)\) (M1)A1
Note: Award A2A0 for (c) and (d) combined, if answers are the wrong way round.
[2 marks]
\(6! = 720\) A2
[2 marks]
any composition of the cycles (1 2), (3 4) and (5 6) (M1)
so \({2^3} = 8\) A1
[2 marks]

