| Date | May 2016 | Marks available | 4 | Reference code | 16M.2.hl.TZ2.11 |
| Level | HL only | Paper | 2 | Time zone | TZ2 |
| Command term | Show that | Question number | 11 | Adapted from | N/A |
Question
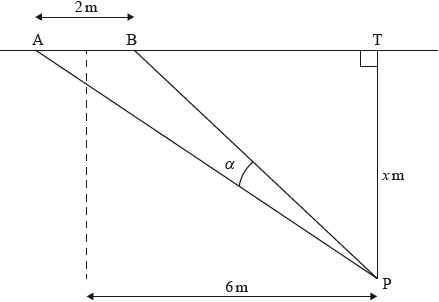
Points A , B and T lie on a line on an indoor soccer field. The goal, [AB] , is 2 metres wide. A player situated at point P kicks a ball at the goal. [PT] is perpendicular to (AB) and is 6 metres from a parallel line through the centre of [AB] . Let PT be \(x\) metros and let \(\alpha = {\rm{A\hat PB}}\) measured in degrees. Assume that the ball travels along the floor.
The maximum for \(\tan \alpha \) gives the maximum for \(\alpha \).
Find the value of \(\alpha \) when \(x = 10\).
Show that \(\tan \alpha = \frac{{2x}}{{{x^2} + 35}}\).
(i) Find \(\frac{{\text{d}}}{{{\text{d}}x}}(\tan \alpha )\).
(ii) Hence or otherwise find the value of \(\alpha \) such that \(\frac{{\text{d}}}{{{\text{d}}x}}(\tan \alpha ) = 0\).
(iii) Find \(\frac{{{{\text{d}}^2}}}{{{\text{d}}{x^2}}}(\tan \alpha )\) and hence show that the value of \(\alpha \) never exceeds 10°.
Find the set of values of \(x\) for which \(\alpha \geqslant 7^\circ \).
Markscheme
EITHER
\(\alpha = \arctan \frac{7}{{10}} - \arctan \frac{5}{{10}}{\text{ }}( = 34.992 \ldots ^\circ - 26.5651 \ldots ^\circ )\) (M1)(A1)(A1)
Note: Award (M1) for \(\alpha = {\rm{A\hat PT}} - {\rm{B\hat PT}}\), (A1) for a correct \({\rm{A\hat PT}}\) and (A1) for a correct \({\rm{B\hat PT}}\).
OR
\(\alpha = \arctan {\text{ }}2 - \arctan \frac{{10}}{7}{\text{ }}( = 63.434 \ldots ^\circ - 55.008 \ldots ^\circ )\) (M1)(A1)(A1)
Note: Award (M1) for \(\alpha = {\rm{P\hat BT}} - {\rm{P\hat AT}}\), (A1) for a correct \({\rm{P\hat BT}}\) and (A1) for a correct \({\rm{P\hat AT}}\).
OR
\(\alpha = \arccos \left( {\frac{{125 + 149 - 4}}{{2 \times \sqrt {125} \times \sqrt {149} }}} \right)\) (M1)(A1)(A1)
Note: Award (M1) for use of cosine rule, (A1) for a correct numerator and (A1) for a correct denominator.
THEN
\( = 8.43^\circ \) A1
[4 marks]
EITHER
\(\tan \alpha = \frac{{\frac{7}{x} - \frac{5}{x}}}{{1 + \left( {\frac{7}{x}} \right)\left( {\frac{5}{x}} \right)}}\) M1A1A1
Note: Award M1 for use of \(\tan (A - B)\), A1 for a correct numerator and A1 for a correct denominator.
\( = \frac{{\frac{2}{x}}}{{1 + \frac{{35}}{{{x^2}}}}}\) M1
OR
\(\tan \alpha = \frac{{\frac{x}{5} - \frac{x}{7}}}{{1 + \left( {\frac{x}{5}} \right)\left( {\frac{x}{7}} \right)}}\) M1A1A1
Note: Award M1 for use of xxx, A1 for a correct numerator and A1 for a correct denominator.
\( = \frac{{\frac{{2x}}{{35}}}}{{1 + \frac{{{x^2}}}{{35}}}}\) M1
OR
\(\cos \alpha = \frac{{{x^2} + 35}}{{\sqrt {({x^2} + 25)({x^2} + 49)} }}\) M1A1
Note: Award M1 for either use of the cosine rule or use of \(\cos (A - B)\).
\(\sin \alpha \frac{{2x}}{{\sqrt {({x^2} + 25)({x^2} + 49)} }}\) A1
\(\tan \alpha = \frac{{\frac{{2x}}{{\sqrt {({x^2} + 25)({x^2} + 49)} }}}}{{\frac{{{x^2} + 35}}{{\sqrt {({x^2} + 25)({x^2} + 49)} }}}}\) M1
THEN
\(\tan \alpha = \frac{{2x}}{{{x^2} + 35}}\) AG
[4 marks]
(i) \(\frac{{\text{d}}}{{{\text{d}}x}}(\tan \alpha ) = \frac{{2({x^2} + 35) - (2x)(2x)}}{{{{({x^2} + 35)}^2}}}{\text{ }}\left( { = \frac{{70 - 2{x^2}}}{{{{({x^2} + 35)}^2}}}} \right)\) M1A1A1
Note: Award M1 for attempting product or quotient rule differentiation, A1 for a correct numerator and A1 for a correct denominator.
(ii) METHOD 1
EITHER
\(\frac{{\text{d}}}{{{\text{d}}x}}(\tan \alpha ) = 0 \Rightarrow 70 - 2{x^2} = 0\) (M1)
\(x = \sqrt {35} {\text{ (m) }}\left( { = 5.9161 \ldots {\text{ (m)}}} \right)\) A1
\(\tan \alpha = \frac{1}{{\sqrt {35} }}{\text{ }}( = 0.16903 \ldots )\) (A1)
OR
attempting to locate the stationary point on the graph of
\(\tan \alpha = \frac{{2x}}{{{x^2} + 35}}\) (M1)
\(x = 5.9161 \ldots {\text{ (m) }}\left( { = \sqrt {35} {\text{ (m)}}} \right)\) A1
\(\tan \alpha = 0.16903 \ldots {\text{ }}\left( { = \frac{1}{{\sqrt {35} }}} \right)\) (A1)
THEN
\(\alpha = 9.59^\circ \) A1
METHOD 2
EITHER
\(\alpha = \arctan \left( {\frac{{2x}}{{{x^2} + 35}}} \right) \Rightarrow \frac{{{\text{d}}\alpha }}{{{\text{d}}x}} = \frac{{70 - 2{x^2}}}{{{{({x^2} + 35)}^2} + 4{x^2}}}\) M1
\(\frac{{{\text{d}}\alpha }}{{{\text{d}}x}} = 0 \Rightarrow x = \sqrt {35} {\text{ (m) }}\left( { = 5.9161{\text{ (m)}}} \right)\) A1
OR
attempting to locate the stationary point on the graph of
\(\alpha = \arctan \left( {\frac{{2x}}{{{x^2} + 35}}} \right)\) (M1)
\(x = 5.9161 \ldots {\text{ (m) }}\left( { = \sqrt {35} {\text{ (m)}}} \right)\) A1
THEN
\(\alpha = 0.1674 \ldots {\text{ }}\left( { = \arctan \frac{1}{{\sqrt {35} }}} \right)\) (A1)
\( = 9.59^\circ \) A1
(iii) \(\frac{{{{\text{d}}^2}}}{{{\text{d}}{x^2}}}(\tan \alpha ) = \frac{{{{({x^2} + 25)}^2}( - 4x) - (2)(2x)({x^2} + 35)(70 - 2{x^2})}}{{{{({x^2} + 35)}^4}}}{\text{ }}\left( { = \frac{{4x({x^2} - 105)}}{{{{({x^2} + 35)}^3}}}} \right)\) M1A1
substituting \(x = \sqrt {35} {\text{ }}( = 5.9161 \ldots )\) into \(\frac{{{{\text{d}}^2}}}{{{\text{d}}{x^2}}}(\tan \alpha )\) M1
\(\frac{{{{\text{d}}^2}}}{{{\text{d}}{x^2}}}(\tan \alpha ) < 0{\text{ }}( =- 0.004829 \ldots )\) and so \(\alpha = 9.59^\circ \) is the maximum value of \(\alpha \) R1
\(\alpha \) never exceeds 10° AG
[11 marks]
attempting to solve \(\frac{{2x}}{{{x^2} + 35}} \geqslant \tan 7^\circ \) (M1)
Note: Award (M1) for attempting to solve \(\frac{{2x}}{{{x^2} + 35}} = \tan 7^\circ \).
\(x = 2.55\) and \(x = 13.7\) (A1)
\(2.55 \leqslant x \leqslant 13.7{\text{ (m)}}\) A1
[3 marks]
Examiners report
This question was generally accessible to a large majority of candidates. It was pleasing to see a number of different (and quite clever) trigonometric methods successfully employed to answer part (a) and part (b).
This question was generally accessible to a large majority of candidates. It was pleasing to see a number of different (and quite clever) trigonometric methods successfully employed to answer part (a) and part (b).
The early parts of part (c) were generally well done. In part (c) (i), a few candidates correctly found \(\frac{{\text{d}}}{{{\text{d}}x}}(\tan \alpha )\) in unsimplified form but then committed an algebraic error when endeavouring to simplify further. A few candidates merely stated that \(\frac{{\text{d}}}{{{\text{d}}x}}(\tan \alpha ) = {\sec ^2}\alpha \).
Part (c) (ii) was reasonably well done with a large number of candidates understanding what was required to find the correct value of \(\alpha \) in degrees. In part (c)(iii), a reasonable number of candidates were able to successfully find \(\frac{{{{\text{d}}^2}}}{{{\text{d}}{x^2}}}(\tan \alpha )\) in unsimplified form. Some however attempted to solve \(\frac{{{{\text{d}}^2}}}{{{\text{d}}{x^2}}}(\tan \alpha ) = 0\) for \(\chi \) rather than examine the value of \(\frac{{{{\text{d}}^2}}}{{{\text{d}}{x^2}}}(\tan \alpha )\) at \(x = \sqrt {35} \).
Part (d), which required use of a GCD to determine an inequality, was surprisingly often omitted by candidates. Of the candidates who attempted this part, a number stated that \(x \geqslant 2.55\). Quite a sizeable proportion of candidates who obtained the correct inequality did not express their answer to 3 significant figures.

