| Date | May 2014 | Marks available | 3 | Reference code | 14M.2.HL.TZ2.6 |
| Level | Higher level | Paper | Paper 2 | Time zone | Time zone 2 |
| Command term | Show that | Question number | 6 | Adapted from | N/A |
Question
This question is in two parts. Part 1 is about the use of renewable energy sources. Part 2 is about the gravitational potential of the Earth.
Part 2 Gravitational potential of the Earth
A satellite of mass 780 kg is put into circular orbit \(4.0 \times {10^3}{\text{ km}}\) above the surface of the Earth. It is then moved to a higher orbit \(3.2 \times {10^4}{\text{ km}}\) above the surface.
Calculate, for the satellite as it is moved from the lower orbit to the higher orbit, the change in
The table gives the gravitational potential V for various distances r from the surface of Earth. The radius of Earth is \(6.4 \times {10^3}{\text{ km}}\).
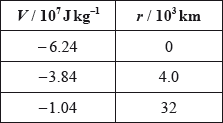
Show that the data are consistent with Earth acting as a point mass with its mass concentrated at its centre.
(i) the gravitational potential energy.
(ii) kinetic energy
(iii) total energy.
Markscheme
recognize that \(V \times \) a distance is constant / \(\frac{{{V_1}}}{{{V_2}}} = \frac{{{R_2}}}{{{R_1}}}{\text{ (}} = 1.625)\);
use of \({R_E} + r\);
evaluates at least two data points \(4.0 \times {10^{14}}\); } (allow \(V \times R\) to be expressed in any consistent unit)
Award [2 max] if answer fails to use radius of Earth but infers wrong conclusion from correct evaluation of two or more data points.
Award [3 max] if answer evaluates mass of Earth and shows that it is the same for two or more data points.
(i) change in gravitational potential \( = ( + )28{\text{ }}({\text{MJ}}\,{\text{k}}{{\text{g}}^{ - 1}})\);
change in gravitational potential energy \( = (28 \times {10^6} \times 780 = ){\text{ }}2.2 \times {10^{10}}{\text{ (J)}}\);
Award [2] for a bald correct answer.
(ii) (change in) \(\frac{1}{2}m{v^2} = \) (change in) \(\frac{{GMm}}{2}{\text{ }}\left( { = - {\text{change in }}\frac{{mV}}{2}} \right)\);
\(( - )1.1 \times {10^{10}}{\text{ (J)}}\);
Award [2] for a bald correct answer.
(iii) change in kinetic energy \( = - 1.1 \times {10^{10}}{\text{ (J)}}\); (recognition that KE is lost)
change in gravitational potential energy \( = + 2.2 \times {10^{10}}{\text{ (J)}}\); } recognition that gpe is gained)
\(( + )1.1 \times {10^{10}}{\text{ (J)}}\); (direction of change required for this mark)
Award [1 max] for a bald correct answer with sign.
Award [0] for a bald correct answer with no sign.
or
change in total energy = change in potential energy + change in kinetic energy;
adds (e)(i) to (e)(ii); (allow ECF in value and sign)
\(( + )1.1 \times {10^{10}}{\text{ (J)}}\); (do not allow negative answer)
Accept correct answer only without ECF for this approach.
Examiners report
This was a simple test to establish whether candidates could check the consistency of data. Most could not. The obvious solution (to evaluate Vr twice having first incorporated the radius of the Earth) was rare. Many candidates preferred to calculate the mass of the earth twice and check that the values obtained were similar. In principle this could have scored full marks but three marks were only rarely seen by examiners.
(i) It is quite clear that candidates do not understand the relationship between gravitational potential and gravitational potential energy. A consideration of units could have led them in the correct direction. Many could only tackle this by carrying out a full solution from the gravitational potential equation printed in the data booklet.
(ii) Similarly candidates were unable to use the known change in gravitational potential energy to establish the change in kinetic energy. Most felt that they had to calculate the kinetic energies from first principles and usually obtained the wrong answer.
(iii) Most candidates did not continue from (i) and (ii) to this part question; it was either left blank or an attempt was made at a statement of conservation of energy. This was another case where knowledge of a principle does not necessarily mean that a candidate can operate it effectively. Even the most able candidates seemed to struggle with this standard piece of bookwork.

