| Date | November 2010 | Marks available | 5 | Reference code | 10N.2.HL.TZ0.B4 |
| Level | Higher level | Paper | Paper 2 | Time zone | Time zone 0 |
| Command term | Calculate and Show that | Question number | B4 | Adapted from | N/A |
Question
This question is in two parts. Part 1 is about collisions. Part 2 is about the gravitational field of Mars.
Part 1 Collisions
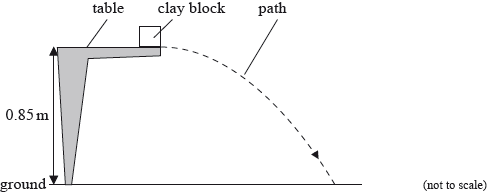
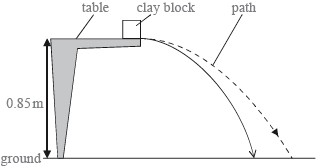
The experiment is repeated with the clay block placed at the edge of the table so that it is fired away from the table. The initial speed of the clay block is \({\text{4.3 m}}\,{{\text{s}}^{ - 1}}\) horizontally. The table surface is 0.85 m above the ground.
Part 2 Gravitational field of Mars
The graph shows the variation with distance \(r\) from the centre of Mars of the gravitational potential \(V\). \(R\) is the radius of Mars which is 3.3 Mm. (Values of \(V\) for \(r < R\) are not shown.)
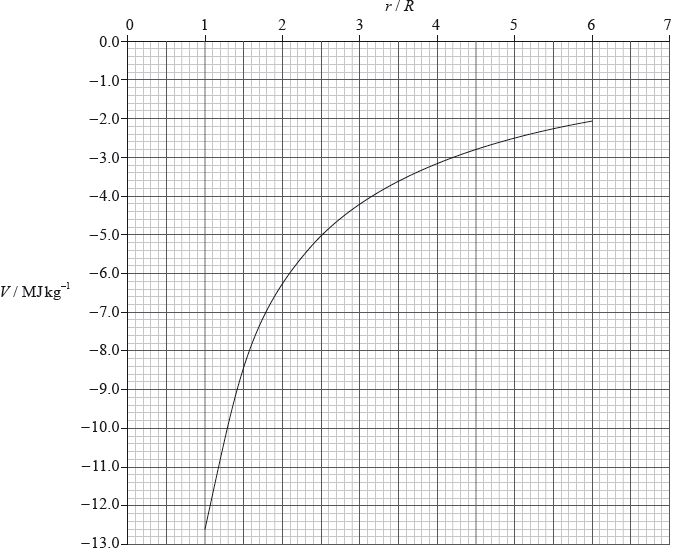
A rocket of mass \(1.2 \times {10^4}{\text{ kg}}\) lifts off from the surface of Mars. Use the graph to
(i) Ignoring air resistance, calculate the horizontal distance travelled by the clay block before it strikes the ground.
(ii) The diagram in (c) shows the path of the clay block neglecting air resistance. On the diagram, draw the approximate shape of the path that the clay block will take assuming that air resistance acts on the clay block.
Define gravitational potential energy of a mass at a point.
(i) calculate the change in gravitational potential energy of the rocket at a distance 4R from the centre of Mars.
(ii) show that the magnitude of the gravitational field strength at a distance 4R from the centre of Mars is \({\text{0.23 N}}\,{\text{k}}{{\text{g}}^{ - 1}}\).
Markscheme
(i) use of kinematic equation to yield time;
\(t = \sqrt {\frac{{2s}}{g}} {\text{ (}} = 0.42{\text{ s)}}\);
\(s = {\text{horizontal speed\( \times \)time}}\);
\( = 1.8{\text{ m}}\);
Accept g = 10 m\(\,\)s\(^{ - 2}\) equivalent answers 1.79 from 9.8, 1.77 from 10.
(ii) initial drawn velocity horizontal; (judge by eye)
reasonable shape; (i.e. quasi-parabolic)
horizontal distance moved always decreasing when compared to given path / range less than original;
work done in moving mass from infinity to a point;
(i) read offs \( - 12.6\) and \( - 3.2\);
gain in \({\text{gpe }}1.2 \times {10^4} \times [12.6 - 3.2]\) or gain in g potential \(\left[ {12.6 \times {{10}^6} - 3.2 \times {{10}^6}} \right]\);
\( = 1.13 \pm 0.05 \times {10^5}{\text{ MJ}}\) or \(1.13 \pm 0.05 \times {10^{11}}{\text{ J}}\);
(ii) use of gradient of graph to determine \(g\);
values substituted from drawn gradient \(\left( {{\text{typically }}\frac{{6.7 \times {{10}^6}}}{{7 \times 3.3 \times {{10}^6}}}} \right)\);
\( = 0.23{\text{ N}}\,{\text{k}}{{\text{g}}^{ - 1}}\) (allow answers in the range of 0.20 to 0.26 N\(\,\)kg–1)
Award [0] for solutions from \(\frac{V}{r}\).
Examiners report
(i) Candidates were required to determine the time taken to fall to the floor and then use this time to evaluate the distance travelled horizontally. Many managed this with more or less success.
(ii) Many candidates produced poor attempts at the sketch. Initial trajectories were not horizontal and the general shapes of the curves were usually not quasi-parabolic.
Some candidates gave a definition of gravitational potential, i.e. they related the energy to that of a unit mass.
Throughout this part candidates were instructed to use the graph, those who used other non-graphical methods were penalised.
(i) There were many good evaluations with complete and well presented solutions.
(ii) Use of the Data Booklet equation for gravitational field strength without reference to the graph was common.

