| Date | November 2014 | Marks available | 2 | Reference code | 14N.2.SL.TZ0.4 |
| Level | Standard level | Paper | Paper 2 | Time zone | Time zone 0 |
| Command term | Sketch | Question number | 4 | Adapted from | N/A |
Question
This question is in two parts. Part 1 is about the motion of a ship. Part 2 is about melting ice.
Part 1 Motion of a ship
Some cargo ships use kites working together with the ship’s engines to move the vessel.
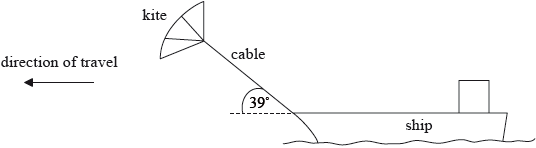
The tension in the cable that connects the kite to the ship is 250 kN. The kite is pulling the ship at an angle of 39° to the horizontal. The ship travels at a steady speed of \({\text{8.5 m}}\,{{\text{s}}^{ - 1}}\) when the ship’s engines operate with a power output of 2.7 MW.
The ship’s engines are switched off and the ship comes to rest from a speed of \({\text{7 m}}\,{{\text{s}}^{ - 1}}\) in a time of 650 s.
Part 2 Melting ice
A container of negligible mass, isolated from its surroundings, contains 0.150 kg of ice at a temperature of –18.7 °C. An electric heater supplies energy at a rate of 125 W.
Outline the meaning of work.
Calculate the work done on the ship by the kite when the ship travels a distance of 1.0 km.
Show that, when the ship is travelling at a speed of \({\text{8.5 m}}\,{{\text{s}}^{ - 1}}\), the kite provides about 40% of the total power required by the ship.
The kite is taken down and no longer produces a force on the ship. The resistive force \(F\) that opposes the motion of the ship is related to the speed \(v\) of the ship by
\[F = k{v^2}\]
where \(k\) is a constant.
Show that, if the power output of the engines remains at 2.7 MW, the speed of the ship will decrease to about \({\text{7 m}}\,{{\text{s}}^{ - 1}}\). Assume that \(k\) is independent of whether the kite is in use or not.
Estimate the distance that the ship takes to stop. Assume that the acceleration is uniform.
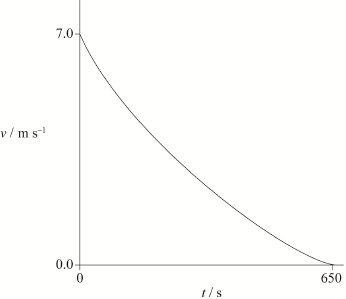
It is unlikely that the acceleration of the ship will be uniform given that the resistive force acting on the ship depends on the speed of the ship. Using the axes, sketch a graph to show how the speed \(v\) varies with time \(t\) after the ship’s engines are switched off.
Describe, with reference to molecular behaviour, the process of melting ice.
After a time interval of 45.0 s all of the ice has reached a temperature of 0 °C without any melting. Calculate the specific heat capacity of ice.
The following data are available.
Specific heat capacity of water \( = 4200{\text{ J}}\,{\text{k}}{{\text{g}}^{ - 1}}{{\text{K}}^{ - 1}}\)
Specific latent heat of fusion of ice \( = 3.30 \times {10^5}{\text{ J}}\,{\text{k}}{{\text{g}}^{ - 1}}\)
Determine the final temperature of the water when the heater supplies energy for a further 600 s.
The whole of the experiment in (f)(i) and (f)(ii) is repeated with a container of negligible mass that is not isolated from the surroundings. The temperature of the surroundings is 18 °C. Comment on the final temperature of the water in (f)(ii).
Markscheme
\({\text{work done}} = {\text{force}} \times {\text{distance moved}}\);
(distance moved) in direction of force;
or
energy transferred;
from one location to another;
or
\({\text{work done}} = Fs\cos \theta \);
with each symbol defined;
\({\text{horizontal force}} = 250\,000 \times \cos 39^\circ {\text{ }}( = 1.94 \times {10^5}{\text{ N}})\);
\({\text{work done}} = 1.9 \times {10^8}{\text{ J}}\);
\({\text{power provided by kite}} = (1.94 \times {10^5} \times 8.5 = ){\text{ }}1.7 \times {10^6}{\text{ W}}\);
\({\text{total power}} = (2.7 + 1.7) \times {10^6}{\text{ W }}( = 4.4 \times {10^6}{\text{ W}})\);
\({\text{fraction provided by kite}} = \frac{{1.7}}{{2.7 + 1.7}}\);
38% or 0.38; (must see answer to 2+ sig figs as answer is given)
Allow answers in the range of 37 to 39% due to early rounding.
or
Award [3 max] for a reverse argument such as:
if 2.7 MW is 60%;
then kite power is \(\frac{2}{3} \times 2.7{\text{ MW}} = 1.8{\text{ MW}}\);
shows that kite power is actually 1.7 MW; (QED)
\(P = (k{v^2}) \times v = k{v^3}\);
\(\frac{{{v_1}}}{{{v_2}}} = \left( {\sqrt[3]{{\left( {\frac{{{P_1}}}{{{P_2}}}} \right)}} = } \right){\text{ }}\sqrt[3]{{\left( {\frac{{7.7}}{{4.4}}} \right)}}\);
\({\text{final speed of ship}} = 7.2{\text{ m}}\,{{\text{s}}^{ - 1}}\); (at least 2 sig figs required).
Approximate answer given, marks are for working only.
correct substitution of 7 or 7.2 into appropriate kinematic equation;
an answer in the range of 2200 to 2400 m;
starts at \(7.0/7.2{\text{ m}}\,{{\text{s}}^{ - 1}}\); (allow ECF from (d)(i))
correct shape;
in ice, molecules vibrate about a fixed point;
as their total energy increases, the molecules (partly) overcome the attractive force between them;
in liquid water the molecules are able to migrate/change position;
\((Q = ){\text{ }}45.0 \times 125{\text{ }}( = 5625{\text{ J}})\);
\(c = \left( {\frac{Q}{{m\Delta \theta }} = } \right){\text{ }}2.01 \times {10^3}{\text{ J}}\,{\text{k}}{{\text{g}}^{ - 1}}{{\text{K}}^{ - 1}}\);
\({\text{energy available}} = 125 \times 600{\text{ }}( = 75000{\text{ J}})\);
\({\text{energy available to warm the water}} = 75000 - [0.15 \times 3.3 \times {10^5}]{\text{ }}( = 25500{\text{ J}})\);
\({\text{temperature}} = \left( {\frac{{25500}}{{0.15 \times 4200}} = } \right){\rm{ 40.5 ^\circ C}}\);
ice/water spends more time below 18 °C;
so net energy transfer is in to the system;
so final water temperature is higher;
or
ice/water spends less time below 18 °C;
so net energy transfer is out of the system;
so final water temperature is lower;
Examiners report
This is a “show that” question which means that the candidate is obliged to show their line of reasoning. Very few SL candidates did this.
This was easy using proportionality, but most candidates at SL attempted to calculate k unnecessarily. Even so there were many correct answers.
A minority of candidates knew that molecules made a transition from being localised to being free to migrate, but had difficulty expressing their answers coherently. Candidates are so used to commenting on the energy transformations when ice melts, that many completely misread the question.
Many good answers, although those that did not get the correct answers presented their working in such a way that part marks (ECF) were not able to be given.
Many good answers, although those that did not get the correct answers presented their working in such a way that part marks (ECF) were not able to be given.
The significance of the temperature of the surroundings was ignored by nearly all candidates, but most were able to obtain 2 marks for suggesting that thermal energy would be lost to the surroundings causing a lower final temperature.

