| Date | November 2015 | Marks available | 3 | Reference code | 15N.2.HL.TZ0.4 |
| Level | Higher level | Paper | Paper 2 | Time zone | Time zone 0 |
| Command term | Compare | Question number | 4 | Adapted from | N/A |
Question
This question is about an ideal gas.
The graph shows how the pressure \(P\) of a sample of fixed mass of an ideal gas varies with volume \(V\).
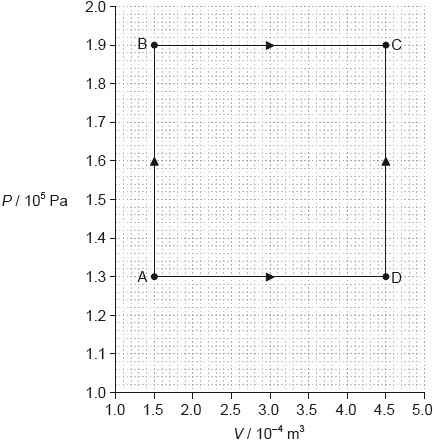
The temperature of the gas at point A is 85 °C. The gas can change its state to that of point C either along route ABC or route ADC.
Calculate the temperature of the gas at point C.
Compare, without any calculation, the work done and the thermal energy supplied along route ABC and route ADC.
Markscheme
use of \(\frac{{PV}}{T} = \) constant or use of \(T \propto PV\) or via intermediate calculation of \(n\) in \(PV = nRT\);
\(\frac{{1.95}}{{358}} = \frac{{8.55}}{{{T_{\text{c}}}}}\) or \(n = 6.55 \times {10^{ - 3}}{\text{ (mol)}}\); } (allow power of ten omission provided same omission on both sides)
1570 K or 1300 °C;
Award [3] for a bald correct answer ignoring small rounding errors.
Omitting conversion to Kelvin yields answer of 373 – award [2 max] as one error.
Award [1 max] if 273 subsequently added (to give 646).
same temperature change so same change in internal energy/\(\Delta U\);
work done along ABC is larger/ADB is smaller because area under ABC is greater than area under ADC/\(\Delta V\) same in both, \(P\) greater for ABC so \(P\Delta V\) also greater for ABC;
because \(\Delta Q = \Delta U + W\) thermal energy transferred is greater for route ABC/smaller for route ADB;
Must see reference to first law for MP3.
Examiners report
It is sad that many young physicists at this level cannot negotiate their way correctly through a straightforward gas-law calculation. As usual, many failed to convert from degree Celsius to Kelvin before carrying out the numerical manipulation. This was an excellent way to lose marks.
A good number were able to give answers to parts of this question but few could pull all the strands together convincingly. Frequent omissions were: to show that the internal energy changes are identical because the endpoint temperatures are the same, and to use the first law to confirm the final linking statement.

