| Date | May 2017 | Marks available | 2 | Reference code | 17M.3.SL.TZ2.11 |
| Level | Standard level | Paper | Paper 3 | Time zone | Time zone 2 |
| Command term | State | Question number | 11 | Adapted from | N/A |
Question
The diagram shows the structure of a typical main sequence star.
Star X is likely to evolve into a neutron star.
State the most abundant element in the core and the most abundant element in the outer layer.
The Hertzsprung–Russell (HR) diagram shows two main sequence stars X and Y and includes lines of constant radius. R is the radius of the Sun.
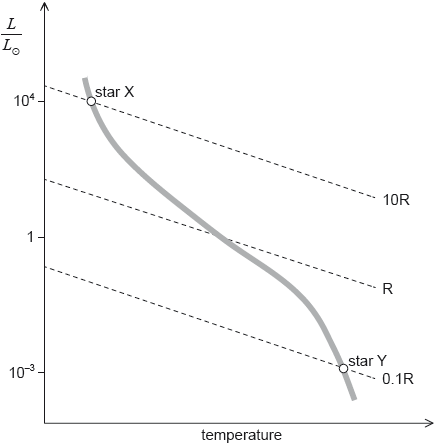
Using the mass–luminosity relation and information from the graph, determine the ratio \(\frac{{{\text{density of star X}}}}{{{\text{density of star Y}}}}\).
On the HR diagram in (b), draw a line to indicate the evolutionary path of star X.
Outline why the neutron star that is left after the supernova stage does not collapse under the action of gravitation.
The radius of a typical neutron star is 20 km and its surface temperature is 106 K. Determine the luminosity of this neutron star.
Determine the region of the electromagnetic spectrum in which the neutron star in (c)(iii) emits most of its energy.
Markscheme
core: helium
outer layer: hydrogen
Accept no other elements.
[2 marks]
ratio of masses is \({\left( {\frac{{{{10}^4}}}{{{{10}^{ - 3}}}}} \right)^{\frac{1}{{3.5}}}} = {10^2}\)
ratio of volumes is \({\left( {\frac{{10}}{{{{10}^{ - 1}}}}} \right)^3} = {10^6}\)
so ratio of densities is \(\frac{{{{10}^2}}}{{{{10}^6}}} = {10^{ - 4}}\)
Allow ECF for MP3 from earlier MPs
[3 marks]
line to the right of X, possibly undulating, very roughly horizontal
Ignore any paths beyond this as the star disappears from diagram.
[1 mark]
gravitation is balanced by a pressure/force due to neutrons/neutron degeneracy/pauli exclusion principle
Do not accept electron degeneracy.
[1 mark]
L = \(\sigma \)AT 4 = 5.67 x 10–8 x 4\(\pi \) x (2.0 x 104)2 x (106)4
L = 3 x 1026 «W»
OR
L = 2.85 x 1026 «W»
Allow ECF for [1 max] if \(\pi \)r 2 used (gives 7 x 1026 «W »)
Allow ECF for a POT error in MP1.
[2 marks]
\(\lambda = \frac{{2.9 \times {{10}^{ - 3}}}}{{{{10}^6}}} = 2.9 \times {10^{ - 9}}\) «m»
this is an X-ray wavelength
[2 marks]

