| Date | November 2010 | Marks available | 4 | Reference code | 10N.2.HL.TZ0.B1 |
| Level | Higher level | Paper | Paper 2 | Time zone | Time zone 0 |
| Command term | Explain | Question number | B1 | Adapted from | N/A |
Question
This question is in two parts. Part 1 is about the simple pendulum. Part 2 is about the de Broglie hypothesis.
Part 2 de Broglie hypothesis
A beam of electrons is accelerated from rest through a potential difference of 85 V.
Show that the de Broglie wavelength associated with the electrons in the beam is 0.13 nm.
Electrons with the same kinetic energy as those in (b) are incident on a circular aperture of diameter 1.1 nm.
The electrons are detected beyond the aperture.
The graph shows the variation with angle \(\theta \) of the number n of electrons detected per second after diffraction by the aperture.
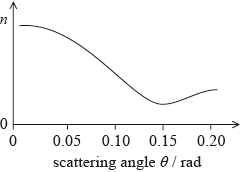
Use your answer to (b) opposite to explain how data from the graph support the de Broglie hypothesis.
Markscheme
\({\text{KE of electron}} = 1.4 \times {10^{ - 17}}{\text{ J}}\);
combine \(\lambda = \frac{h}{p}\) and \({E_{\text{k}}} = \frac{{{p^2}}}{{2m}}\) to get \({\lambda ^2} = \frac{{{h^2}}}{{2m{E_k}}}\);
\({\lambda ^2} = \frac{{{{\left[ {6.6 \times {{10}^{ - 34}}} \right]}^2}}}{{2 \times 9.1 \times {{10}^{ - 31}} \times 1.4 \times {{10}^{ - 17}}}}\);
\(\lambda = 1.3 \times {10^{ - 10}}{\text{ m}}\)
or
\(v = \sqrt {\frac{{2eV}}{m}} \);
\(p = \sqrt {2meV} \);
\(\lambda = \left( {\frac{h}{{\sqrt {2meV} }} = } \right){\text{ }}\frac{{6.6 \times {{10}^{ - 34}}}}{{\sqrt {2 \times 9.1 \times {{10}^{ - 31}} \times 1.6 \times {{10}^{ - 19}} \times 85} }}\);
\(\lambda = 1.3 \times {10^{ - 10}}{\text{ m}}\)
minimum read-off at 0.15 rad; (allow answers in the range of 0.14 rad to 0.16 rad)
\(\lambda = \frac{{b{\theta _{{\text{min}}}}}}{{1.22}}\);
\( = 1.4 \times {10^{ - 10}}{\text{ m}}\);
same/similar wavelength to (b) (so de Broglie hypothesis supported);
Allow [3 max] if 1.22 missing – answer is then 0.162 nm.
Examiners report
Candidates answered this well and had been well schooled in the demands of this calculation. However a significant number wrote solutions that were completely unintelligible to the examiners.
Candidates were required to use the graph of electron beam intensity against scattering angle to show that the scattering aperture diameter was commensurate with the electron wavelength. About half the candidates could achieve this, but some lost marks through omitting the 1.22 factor in the circular aperture equation.

