| Date | November 2010 | Marks available | 3 | Reference code | 10N.2.hl.TZ0.7 |
| Level | HL | Paper | 2 | Time zone | TZ0 |
| Command term | Identify, Predict, and Suggest | Question number | 7 | Adapted from | N/A |
Question
Hydrazine, N2H4, is a valuable rocket fuel.
The equation for the reaction between hydrazine and oxygen is given below.
\[{{\text{N}}_2}{{\text{H}}_4}({\text{l)}} + {{\text{O}}_2}({\text{g)}} \to {{\text{N}}_2}({\text{g)}} + 2{{\text{H}}_2}{\text{O(l)}}\]
The reaction between \({{\text{N}}_2}{{\text{H}}_4}({\text{aq)}}\) and \({\text{HCl(aq)}}\) can be represented by the following equation.
\[{{\text{N}}_2}{{\text{H}}_4}({\text{aq)}} + 2{\text{HCl(aq)}} \to {{\text{N}}_2}{\text{H}}_6^{2 + }({\text{aq)}} + 2{\text{C}}{{\text{l}}^ - }({\text{aq)}}\]
(i) Draw the Lewis (electron dot) structure for N2H4 showing all valence electrons.
(ii) State and explain the H–N–H bond angle in hydrazine.
Hydrazine and ethene, C2H4, are hydrides of adjacent elements in the periodic table. The boiling point of hydrazine is much higher than that of ethene. Explain this difference in terms of the intermolecular forces in each compound.
(i) The enthalpy change of formation, \(\Delta H_{\text{f}}^\Theta \), of liquid hydrazine is \({\text{50.6 kJ}}\,{\text{mo}}{{\text{l}}^{ - 1}}\). Use this value, together with data from Table 12 of the Data Booklet, to calculate the enthalpy change for this reaction.
(ii) Use the bond enthalpy values from Table 10 of the Data Booklet to determine the enthalpy change for this reaction.
(iii) Identify the calculation that produces the most accurate value for the enthalpy change for the reaction given and explain your choice.
(iv) Calculate \(\Delta {S^\Theta }\) for the reaction using the data below and comment on its magnitude.
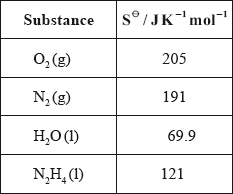
(v) Calculate \(\Delta {G^\Theta }\) for the reaction at 298 K.
(vi) Predict, giving a reason, the spontaneity of the reaction above at both high and low temperatures.
The reaction between \({{\text{N}}_{\text{2}}}{{\text{H}}_{\text{4}}}{\text{(aq)}}\) and HCl(aq) can be represented by the following equation.
\[{{\text{N}}_2}{{\text{H}}_4}({\text{aq)}} + 2{\text{HCl(aq)}} \to {{\text{N}}_2}{\text{H}}_6^{2 + }({\text{aq)}} + 2{\text{C}}{{\text{l}}^ - }({\text{aq)}}\]
(i) Identify the type of reaction that occurs.
(ii) Predict the value of the H–N–H bond angle in \({{\text{N}}_{\text{2}}}{\text{H}}_{\text{6}}^{{\text{2}} + }\).
(iii) Suggest the type of hybridization shown by the nitrogen atoms in \({{\text{N}}_{\text{2}}}{\text{H}}_{\text{6}}^{{\text{2}} + }\).
Markscheme
(i) 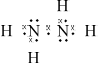 ;
;
Accept x’s, dots or lines for electron pairs
(ii) H–N–H \( < \) 109 / any angle between 104° and 109°;
due to four centres of electron charge / four electron pairs (one of which is a lone \({{\text{e}}^ - }\) pair);
extra repulsion due to lone electron pairs;
Do not allow ECF for wrong Lewis structures.
weaker van der Waals’/London/dispersion/intermolecular forces in ethene;
stronger (intermolecular) hydrogen bonding in hydrazine;
If no comparison between strengths then [1 max].
(i) \(\Delta H_{\text{r}}^\Theta = \Sigma \Delta H_{\text{f}}^\Theta {\text{ products}} - \Sigma \Delta H_{\text{f}}^\Theta {\text{ reactants}}\);
Can be implied by working.
\(\Delta H_{\text{f}}^\Theta {\text{(}}{{\text{H}}_2}{\text{O(l))}} = - 286{\text{ (kJ)}}\);
\(\Delta H_{\text{r}}^\Theta = 2( - 286) - 50.6 = - 622.6{\text{ (kJ)}}\);
(ii) bonds broken: 4N–H, N–N, O=O / \( + {\text{2220 (kJ}}\,{\text{mo}}{{\text{l}}^{ - 1}}{\text{)}}\);
bonds formed: N\(\equiv\)N, 4O-H / \( - 2801{\text{ (kJ}}\,{\text{mo}}{{\text{l}}^{ - 1}}{\text{)}}\);
\( - 581{\text{ (kJ}}\,{\text{mo}}{{\text{l}}^{ - 1}}{\text{)}}\);
Award [3] for correct final answer.
(iii) value based on \(\Delta {H_{\text{f}}}\) more accurate;
\(\Delta {H_{\text{f}}}\) accurate for compounds in reaction;
bond energy calculation assumes average bond energies;
(bond energy calculation) only applies to gaseous states / ignores intermolecular bonds;
(iv) \(\Delta {S^\Theta } = \Sigma {S^\Theta }{\text{ (products)}} - \Sigma {S^\Theta }{\text{ (reactants)}}\);
Can be implied by working.
\( = 191 + (2 \times 69.9) - 205 - 121 = + 4.8{\text{ (J}}\,{{\text{K}}^{ - 1}}{\text{mo}}{{\text{l}}^{ - 1}}{\text{)}}\);
small value since number of mol of g on both sides the same;
(v) \(\Delta {G^\Theta } = - 622.6 - 298(0.0048)\);
\( = - 624.0{\text{ (kJ}}\,{\text{mo}}{{\text{l}}^{ - 1}}{\text{)}}\);
Allow 623.9 to 624.1.
(vi) all reactions are spontaneous;
\(\Delta G\) is negative (at high temperatures and low temperatures);
(i) acid-base/neutralization;
(ii) 109°/109.5°;
(iii) sp3;
No ECF if bond angle incorrect in (ii).
Examiners report
The Lewis structure for hydrazine proved to be difficult for some in (a). Incorrect answers had double bonds appearing between the two nitrogen atoms or lone pairs missing. Those who could draw the correct structure in (i) gave the correct bond angle, but the explanation was often incomplete. Few mentioned either the four electron domains around the central atom or the extra repulsion of the lone pair.
In part (b) most candidates knew that hydrogen bonding was present in hydrazine and Van der Waals‟ forces in ethene but failed to give a comparison of the relative strength of the intermolecular forces.
Some candidates struggled to calculate the enthalpy changes from enthalpy changes of formation in (c) (i) as they were unable to relate the enthalpy change of combustion of hydrogen to the enthalpy change of formation of water.
The bond energy and entropy calculations were more successful with many candidates benefitting from ECF from their incorrect Lewis structures in (a). It was encouraging to see many correct unit conversions for the calculation of \(\Delta G\). A number of candidates incorrectly described the combination of hydrazine and hydrochloric acid as a redox reaction, but many were able to identify the bond angle and hybridization in \({{\text{N}}_{\text{2}}}{\text{H}}_{\text{6}}^{{\text{2}} + }\).

