| Date | May 2010 | Marks available | 3 | Reference code | 10M.2.hl.TZ0.6 |
| Level | HL only | Paper | 2 | Time zone | TZ0 |
| Command term | Find | Question number | 6 | Adapted from | N/A |
Question
The diagram shows a sketch of the graph of \(y = {x^{ - 4}}\) for \(x > 0\) .
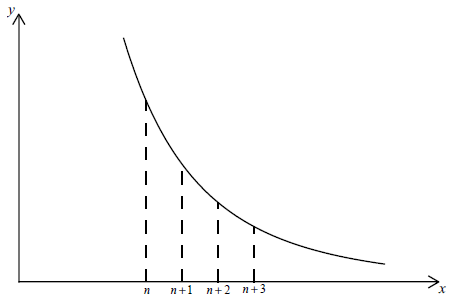
By considering this sketch, show that, for \(n \in {\mathbb{Z}^ + }\) ,\[\sum\limits_{r = n + 1}^\infty {\frac{1}{{{r^4}}}} < \int_n^\infty {\frac{{{\rm{d}}x}}{{{x^4}}}} < \sum\limits_{r = n}^\infty {\frac{1}{{{r^4}}}} .\]
Let \(S = \sum\limits_{r = 1}^\infty {\frac{1}{{{r^4}}}} \) .
Use the result in (a) to show that, for \(n \ge 2\) , the value of \(S\) lies between
\(\sum\limits_{r = 1}^{n - 1} {\frac{1}{{{r^4}}}} + \frac{1}{{3{n^3}}}\) and \(\sum\limits_{r = 1}^n {\frac{1}{{{r^4}}}} + \frac{1}{{3{n^3}}}\) .
(i) Show that, by taking \(n = 8\) , the value of \(S\) can be deduced correct to three decimal places and state this value.
(ii) The exact value of \(S\) is known to be \(\frac{{{\pi ^4}}}{N}\)where \(N \in {\mathbb{Z}^ + }\) . Determine the value of \(N\) .
Now let \(T = \sum\limits_{r = 1}^\infty {\frac{{{{( - 1)}^{r + 1}}}}{{{r^4}}}} \) .
Find the value of \(T\) correct to three decimal places.
Markscheme
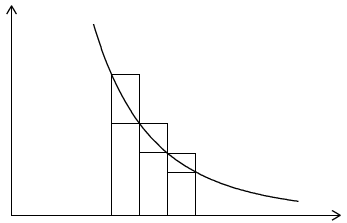 (M1)
(M1)
total area of "upper" rectangles
\( = \frac{1}{{{n^4}}} \times 1 + \frac{1}{{{{(n + 1)}^4}}} \times 1 + \frac{1}{{{{(n + 2)}^4}}} \times 1 + \ldots = \sum\limits_{r = n}^\infty {\frac{1}{{{r^4}}}} \) M1A1
total area of "lower" rectangles
\( = \frac{1}{{{{(n + 1)}^4}}} \times 1 + \frac{1}{{{{(n + 2)}^4}}} \times 1 + \frac{1}{{{{(n + 3)}^4}}} \times 1 + \ldots = \sum\limits_{r = n + 1}^\infty {\frac{1}{{{r^4}}}} \) A1
the total area under the curve from \(x = n\) to infinity lies between these two sums hence \(\sum\limits_{r = n + 1}^\infty {\frac{1}{{{r^4}}}} < \int_n^\infty {\frac{{{\rm{d}}x}}{{{x^4}}}} < \sum\limits_{r = n}^\infty {\frac{1}{{{r^4}}}} \) R1AG
[5 marks]
first evaluate the integral
\(\int_n^\infty {\frac{{{\rm{d}}x}}{{{x^4}}}} = - \left[ {\frac{1}{{3{x^3}}}} \right]_n^\infty = \frac{1}{{3{n^3}}}\) M1A1
it follows that
\(\sum\limits_{r = n + 1}^\infty {\frac{1}{{{r^4}}}} < \frac{1}{{3{n^3}}}\) A1
adding \(\sum\limits_{r = 1}^n {\frac{1}{{{r^4}}}} \) to both sides, M1
\(S < \sum\limits_{r = 1}^n {\frac{1}{{{r^4}}}} + \frac{1}{{3{n^3}}}\) A1
similarly,
\(\sum\limits_{r = n}^\infty {\frac{1}{{{r^4}}}} > \frac{1}{{3{n^3}}}\) A1
adding \(\sum\limits_{r = 1}^{n - 1} {\frac{1}{{{r^4}}}} \) to both sides, M1
\(S > \sum\limits_{r = 1}^{n - 1} {\frac{1}{{{r^4}}}} + \frac{1}{{3{n^3}}}\) A1
hence the value of \(S\) lies between
\(\sum\limits_{r = 1}^{n - 1} {\frac{1}{{{r^4}}}} + \frac{1}{{3{n^3}}}\) and \(\sum\limits_{r = 1}^n {\frac{1}{{{r^4}}}} + \frac{1}{{3{n^3}}}\) AG
[8 marks]
(i) putting \(n = 8\) , we find that
\(S < 1.08243 \ldots \) and \(S > 1.08219 \ldots \) A1A1
it follows that \(S = 1.082\) to 3 decimal places A1
(ii) substituting this value of \(S\),
\(N \approx \frac{{{\pi ^4}}}{{1.082}} \approx 90.0268\) M1A1
\(N = 90\) A1
[6 marks]
EITHER
successive partial sums are
1 M1
0.9375
0.9498…
0.9459…
0.9475…
0.9467…
0.9471… A1
it follows that correct to 3 decimal places \(T = 0.947\) A1
OR
\(T = S - \frac{2}{{16}}S\) M1A1
using part (c)(i) or \(0.94703…\) using the sum given in part (c)(ii) \(0.9471…\)
it follows that \(T = 0.947\) correct to 3 decimal places A1
[3 marks]
Examiners report
Most candidates attempted (a), although in many cases the explanations were poor and unconvincing.
It was pleasing to see that some candidates who were unable to do part (a) moved on and made a reasonable attempt at (b) and (c).
It was pleasing to see that some candidates who were unable to do part (a) moved on and made a reasonable attempt at (b) and (c).
Attempts at (d) were often disappointing with candidates not realising that, in this case, the sum to infinity lies between any two successive partial sums.

