| Date | May 2015 | Marks available | 2 | Reference code | 15M.1.sl.TZ1.3 |
| Level | SL only | Paper | 1 | Time zone | TZ1 |
| Command term | Write down | Question number | 3 | Adapted from | N/A |
Question
The diagram shows the straight line \({L_1}\), which intersects the \(x\)-axis at \({\text{A}}(6,{\text{ }}0)\) and the \(y\)-axis at \({\text{B}}(0,{\text{ }}2)\) .
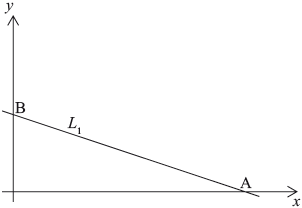
Write down the coordinates of M, the midpoint of line segment AB.
Calculate the gradient of \({L_1}\).
The line \({L_2}\) is parallel to \({L_1}\) and passes through the point \((3,{\text{ }}2)\).
Find the equation of \({L_2}\). Give your answer in the form \(y = mx + c\).
Markscheme
\((3,{\text{ }}1)\) (A1)(A1) (C2)
Note: Accept \(x = 3\), \(y = 1\). Award (A0)(A1) if parentheses are missing.
\(\frac{{2 - 0}}{{0 - 6}}\) (M1)
Note: Award (M1) for correct substitution into gradient formula.
\( = - \frac{1}{3}( - 0.333333 \ldots )\) (A1) (C2)
Note: Accept \( - \frac{2}{6}\).
\((y - 2) = - \frac{1}{3}(x - 3)\) (M1)
OR
\(2 = - \frac{1}{3}(3) + c\) (M1)
Note: Award (M1) for substitution of their gradient from part (b).
\(y = - \frac{1}{3}x + 3\) (A1)(ft) (C2)
Note: Follow through from part (b).
The answer must be an equation in the form \(y = mx + c\) for the (A1)(ft) to be awarded.
Examiners report
Parts (a), finding the midpoint, and (b) finding the gradient, of this question were done well by the majority of candidates.
Parts (a), finding the midpoint, and (b) finding the gradient, of this question were done well by the majority of candidates. Some candidates substituted incorrectly into the gradient formula or reversed the numerator and denominator.
There was a significant number of candidates who calculated the equation of the normal to the given line and not the equation of a parallel line. It seemed those candidates answered the question they expected and not the question asked.

