| Date | November 2013 | Marks available | 4 | Reference code | 13N.2.sl.TZ0.4 |
| Level | SL only | Paper | 2 | Time zone | TZ0 |
| Command term | Sketch | Question number | 4 | Adapted from | N/A |
Question
Consider the function \(f(x) = \frac{3}{4}{x^4} - {x^3} - 9{x^2} + 20\).
Find \(f( - 2)\).
Find \(f'(x)\).
The graph of the function \(f(x)\) has a local minimum at the point where \(x = - 2\).
Using your answer to part (b), show that there is a second local minimum at \(x = 3\).
The graph of the function \(f(x)\) has a local minimum at the point where \(x = - 2\).
Sketch the graph of the function \(f(x)\) for \( - 5 \leqslant x \leqslant 5\) and \( - 40 \leqslant y \leqslant 50\). Indicate on your
sketch the coordinates of the \(y\)-intercept.
The graph of the function \(f(x)\) has a local minimum at the point where \(x = - 2\).
Write down the coordinates of the local maximum.
Let \(T\) be the tangent to the graph of the function \(f(x)\) at the point \((2, –12)\).
Find the gradient of \(T\).
The line \(L\) passes through the point \((2, −12)\) and is perpendicular to \(T\).
\(L\) has equation \(x + by + c = 0\), where \(b\) and \(c \in \mathbb{Z}\).
Find
(i) the gradient of \(L\);
(ii) the value of \(b\) and the value of \(c\).
Markscheme
\(\frac{3}{4}{( - 2)^4} - {( - 2)^3} - 9{( - 2)^2} + 20\) (M1)
Note: Award (M1) for substituting \(x = - 2\) in the function.
\(= 4\) (A1)(G2)
Note: If the coordinates \(( - 2,{\text{ }}4)\) are given as the answer award, at most, (M1)(A0). If no working shown award (G1).
If \(x = - 2,{\text{ }}y = 4\) seen then award full marks.
[2 marks]
\(3{x^3} - 3{x^2} - 18x\) (A1)(A1)(A1)
Note: Award (A1) for each correct term, award at most (A1)(A1)(A0) if extra terms seen.
[3 marks]
\(f'(3) = 3 \times {(3)^3} - 3 \times {(3)^2} - 18 \times 3\) (M1)
Note: Award (M1) for substitution in their \(f'(x)\) of \(x = 3\).
\( = 0\) (A1)
OR
\(3{x^3} - 3{x^2} - 18x = 0\) (M1)
Note: Award (M1) for equating their \(f'(x)\) to zero.
\(x = 3\) (A1)
\(f'({x_1}) = 3 \times {({x_1})^3} - 3 \times {({x_1})^2} - 18 \times {x_1} < 0\) where \(0 < {x_1} < 3\) (M1)
Note: Award (M1) for substituting a value of \({x_1}\) in the range \(0 < {x_1} < 3\) into their \(f'\) and showing it is negative (decreasing).
\(f'({x_2}) = 3 \times {({x_2})^3} - 3 \times {({x_2})^2} - 18 \times {x_2} > 0\) where \({x_2} > 3\) (M1)
Note: Award (M1) for substituting a value of \({x_2}\) in the range \({x_2} > 3\) into their \(f'\) and showing it is positive (increasing).
OR
With or without a sketch:
Showing \(f({x_1}) > f(3)\) where \({x_1} < 3\) and \({x_1}\) is close to 3. (M1)
Showing \(f({x_2}) > f(3)\) where \({x_2} > 3\) and \({x_2}\) is close to 3. (M1)
Note: If a sketch of \(f(x)\) is drawn in this part of the question and \(x = 3\) is identified as a stationary point on the curve, then
(i) award, at most, (M1)(A1)(M1)(M0) if the stationary point has been found;
(ii) award, at most, (M0)(A0)(M1)(M0) if the stationary point has not been previously found.
Since the gradients go from negative (decreasing) through zero to positive (increasing) it is a local minimum (R1)(AG)
Note: Only award (R1) if the first two marks have been awarded ie \(f'(3)\) has been shown to be equal to \(0\).
[5 marks]
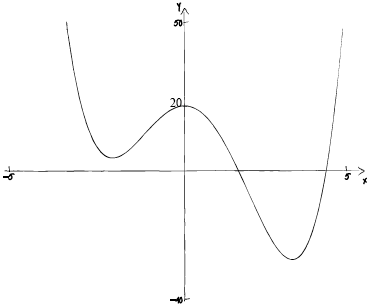 (A1)(A1)(A1)(A1)
(A1)(A1)(A1)(A1)
Notes: Award (A1) for labelled axes and indication of scale on both axes.
Award (A1) for smooth curve with correct shape.
Award (A1) for local minima in \({2^{{\text{nd}}}}\) and \({4^{{\text{th}}}}\) quadrants.
Award (A1) for y intercept \((0, 20)\) seen and labelled. Accept \(20\) on \(y\)-axis.
Do not award the third (A1) mark if there is a turning point on the \(x\)-axis.
If the derivative function is sketched then award, at most, (A1)(A0)(A0)(A0).
For a smooth curve (with correct shape) there should be ONE continuous thin line, no part of which is straight and no (one to many) mappings of \(x\).
[4 marks]
\((0, 20)\) (G1)(G1)
Note: If parentheses are omitted award (G0)(G1).
OR
\(x = 0,{\text{ }}y = 20\) (G1)(G1)
Note: If the derivative function is sketched in part (d), award (G1)(ft)(G1)(ft) for \((–1.12, 12.2)\).
[2 marks]
\(f'(2) = 3{(2)^3} - 3{(2)^2} - 18(2)\) (M1)
Notes: Award (M1) for substituting \(x = 2\) into their \(f'(x)\).
\( = - 24\) (A1)(ft)(G2)
[2 marks]
(i) Gradient of perpendicular \( = \frac{1}{{24}}\) \((0.0417, 0.041666…)\) (A1)(ft)(G1)
Note: Follow through from part (f).
(ii) \(y + 12 = \frac{1}{{24}}(x - 2)\) (M1)(M1)
Note: Award (M1) for correct substitution of \((2, –12)\), (M1) for correct substitution of their perpendicular gradient into equation of line.
OR
\( - 12 = \frac{1}{{24}} \times 2 + d\) (M1)
\(d = - \frac{{145}}{{12}}\)
\(y = \frac{1}{{24}}x - \frac{{145}}{{12}}\) (M1)
Note: Award (M1) for correct substitution of \((2, –12)\) and gradient into equation of a straight line, (M1) for correct substitution of the perpendicular gradient and correct substitution of \(d\)into equation of line.
\(b = - 24,{\text{ }}c = - 290\) (A1)(ft)(A1)(ft)(G3)
Note: Follow through from parts (f) and g(i).
To award (ft) marks, \(b\) and \(c\) must be integers.
Where candidate has used \(0.042\) from g(i), award (A1)(ft) for \(–288\).
[5 marks]
Examiners report
Surprisingly, a correct method for substituting the value of –2 into the given function led many candidates to a variety of incorrect answers. This suggests a poor handling of negative signs and/or poor use of the graphic display calculator. Many correct answers were seen in part (b) as candidates seemed to be well-drilled in the process of differentiation. Part (c), however, proved to be quite a discriminator. There were 5 marks for this part of the question and simply showing that \(x - 3\) is a turning point was not sufficient for all of these marks. Many simply scored only two marks by substituting \(x - 3\) into their answer to part (b). Once they had shown that there was a turning point at \(x - 3\), candidates were not expected to use the second derivative but to show that the function decreases for \(x < 3\) and increases for \(x > 3\). Part (d) required a sketch which could have either been done on lined paper or on graph paper. The majority of candidates obtained at least two marks here with the most common errors seen being incomplete labelled axes and curves which were far from being smooth. In part (e), many candidates identified the correct coordinates for the two marks available. But for many candidates, this is where responses stopped as, in part (f), connecting the gradient function found in part (b) to the given coordinates proved problematic and only a significant minority of candidates were able to arrive at the required answer of –24. Indeed, there were many NR (no responses) to this part and the final part of the question. As many candidates found part (f) difficult, even more candidates found getting beyond the gradient of L very difficult indeed. A minority of candidates wrote down the gradient of their perpendicular but then did not seem to know where to proceed from there. Substituting their gradient for b and the coordinates (2, –12) into the equation \(x + by + c = 0\) was a popular, but erroneous, method. It was a rare event indeed to see a script with a correct answer for this part of the question.
Surprisingly, a correct method for substituting the value of –2 into the given function led many candidates to a variety of incorrect answers. This suggests a poor handling of negative signs and/or poor use of the graphic display calculator. Many correct answers were seen in part (b) as candidates seemed to be well-drilled in the process of differentiation. Part (c), however, proved to be quite a discriminator. There were 5 marks for this part of the question and simply showing that \(x - 3\) is a turning point was not sufficient for all of these marks. Many simply scored only two marks by substituting \(x - 3\) into their answer to part (b). Once they had shown that there was a turning point at \(x - 3\), candidates were not expected to use the second derivative but to show that the function decreases for \(x < 3\) and increases for \(x > 3\). Part (d) required a sketch which could have either been done on lined paper or on graph paper. The majority of candidates obtained at least two marks here with the most common errors seen being incomplete labelled axes and curves which were far from being smooth. In part (e), many candidates identified the correct coordinates for the two marks available. But for many candidates, this is where responses stopped as, in part (f), connecting the gradient function found in part (b) to the given coordinates proved problematic and only a significant minority of candidates were able to arrive at the required answer of –24. Indeed, there were many NR (no responses) to this part and the final part of the question. As many candidates found part (f) difficult, even more candidates found getting beyond the gradient of L very difficult indeed. A minority of candidates wrote down the gradient of their perpendicular but then did not seem to know where to proceed from there. Substituting their gradient for b and the coordinates (2, –12) into the equation \(x + by + c = 0\) was a popular, but erroneous, method. It was a rare event indeed to see a script with a correct answer for this part of the question.
Surprisingly, a correct method for substituting the value of –2 into the given function led many candidates to a variety of incorrect answers. This suggests a poor handling of negative signs and/or poor use of the graphic display calculator. Many correct answers were seen in part (b) as candidates seemed to be well-drilled in the process of differentiation. Part (c), however, proved to be quite a discriminator. There were 5 marks for this part of the question and simply showing that \(x - 3\) is a turning point was not sufficient for all of these marks. Many simply scored only two marks by substituting \(x - 3\) into their answer to part (b). Once they had shown that there was a turning point at \(x - 3\), candidates were not expected to use the second derivative but to show that the function decreases for \(x < 3\) and increases for \(x > 3\). Part (d) required a sketch which could have either been done on lined paper or on graph paper. The majority of candidates obtained at least two marks here with the most common errors seen being incomplete labelled axes and curves which were far from being smooth. In part (e), many candidates identified the correct coordinates for the two marks available. But for many candidates, this is where responses stopped as, in part (f), connecting the gradient function found in part (b) to the given coordinates proved problematic and only a significant minority of candidates were able to arrive at the required answer of –24. Indeed, there were many NR (no responses) to this part and the final part of the question. As many candidates found part (f) difficult, even more candidates found getting beyond the gradient of L very difficult indeed. A minority of candidates wrote down the gradient of their perpendicular but then did not seem to know where to proceed from there. Substituting their gradient for b and the coordinates (2, –12) into the equation \(x + by + c = 0\) was a popular, but erroneous, method. It was a rare event indeed to see a script with a correct answer for this part of the question.
Surprisingly, a correct method for substituting the value of –2 into the given function led many candidates to a variety of incorrect answers. This suggests a poor handling of negative signs and/or poor use of the graphic display calculator. Many correct answers were seen in part (b) as candidates seemed to be well-drilled in the process of differentiation. Part (c), however, proved to be quite a discriminator. There were 5 marks for this part of the question and simply showing that \(x - 3\) is a turning point was not sufficient for all of these marks. Many simply scored only two marks by substituting \(x - 3\) into their answer to part (b). Once they had shown that there was a turning point at \(x - 3\), candidates were not expected to use the second derivative but to show that the function decreases for \(x < 3\) and increases for \(x > 3\). Part (d) required a sketch which could have either been done on lined paper or on graph paper. The majority of candidates obtained at least two marks here with the most common errors seen being incomplete labelled axes and curves which were far from being smooth. In part (e), many candidates identified the correct coordinates for the two marks available. But for many candidates, this is where responses stopped as, in part (f), connecting the gradient function found in part (b) to the given coordinates proved problematic and only a significant minority of candidates were able to arrive at the required answer of –24. Indeed, there were many NR (no responses) to this part and the final part of the question. As many candidates found part (f) difficult, even more candidates found getting beyond the gradient of L very difficult indeed. A minority of candidates wrote down the gradient of their perpendicular but then did not seem to know where to proceed from there. Substituting their gradient for b and the coordinates (2, –12) into the equation \(x + by + c = 0\) was a popular, but erroneous, method. It was a rare event indeed to see a script with a correct answer for this part of the question.
Surprisingly, a correct method for substituting the value of –2 into the given function led many candidates to a variety of incorrect answers. This suggests a poor handling of negative signs and/or poor use of the graphic display calculator. Many correct answers were seen in part (b) as candidates seemed to be well-drilled in the process of differentiation. Part (c), however, proved to be quite a discriminator. There were 5 marks for this part of the question and simply showing that \(x - 3\) is a turning point was not sufficient for all of these marks. Many simply scored only two marks by substituting \(x - 3\) into their answer to part (b). Once they had shown that there was a turning point at \(x - 3\), candidates were not expected to use the second derivative but to show that the function decreases for \(x < 3\) and increases for \(x > 3\). Part (d) required a sketch which could have either been done on lined paper or on graph paper. The majority of candidates obtained at least two marks here with the most common errors seen being incomplete labelled axes and curves which were far from being smooth. In part (e), many candidates identified the correct coordinates for the two marks available. But for many candidates, this is where responses stopped as, in part (f), connecting the gradient function found in part (b) to the given coordinates proved problematic and only a significant minority of candidates were able to arrive at the required answer of –24. Indeed, there were many NR (no responses) to this part and the final part of the question. As many candidates found part (f) difficult, even more candidates found getting beyond the gradient of L very difficult indeed. A minority of candidates wrote down the gradient of their perpendicular but then did not seem to know where to proceed from there. Substituting their gradient for b and the coordinates (2, –12) into the equation \(x + by + c = 0\) was a popular, but erroneous, method. It was a rare event indeed to see a script with a correct answer for this part of the question.
Surprisingly, a correct method for substituting the value of –2 into the given function led many candidates to a variety of incorrect answers. This suggests a poor handling of negative signs and/or poor use of the graphic display calculator. Many correct answers were seen in part (b) as candidates seemed to be well-drilled in the process of differentiation. Part (c), however, proved to be quite a discriminator. There were 5 marks for this part of the question and simply showing that \(x - 3\) is a turning point was not sufficient for all of these marks. Many simply scored only two marks by substituting \(x - 3\) into their answer to part (b). Once they had shown that there was a turning point at \(x - 3\), candidates were not expected to use the second derivative but to show that the function decreases for \(x < 3\) and increases for \(x > 3\). Part (d) required a sketch which could have either been done on lined paper or on graph paper. The majority of candidates obtained at least two marks here with the most common errors seen being incomplete labelled axes and curves which were far from being smooth. In part (e), many candidates identified the correct coordinates for the two marks available. But for many candidates, this is where responses stopped as, in part (f), connecting the gradient function found in part (b) to the given coordinates proved problematic and only a significant minority of candidates were able to arrive at the required answer of –24. Indeed, there were many NR (no responses) to this part and the final part of the question. As many candidates found part (f) difficult, even more candidates found getting beyond the gradient of L very difficult indeed. A minority of candidates wrote down the gradient of their perpendicular but then did not seem to know where to proceed from there. Substituting their gradient for b and the coordinates (2, –12) into the equation \(x + by + c = 0\) was a popular, but erroneous, method. It was a rare event indeed to see a script with a correct answer for this part of the question.
Surprisingly, a correct method for substituting the value of –2 into the given function led many candidates to a variety of incorrect answers. This suggests a poor handling of negative signs and/or poor use of the graphic display calculator. Many correct answers were seen in part (b) as candidates seemed to be well-drilled in the process of differentiation. Part (c), however, proved to be quite a discriminator. There were 5 marks for this part of the question and simply showing that \(x - 3\) is a turning point was not sufficient for all of these marks. Many simply scored only two marks by substituting \(x - 3\) into their answer to part (b). Once they had shown that there was a turning point at \(x - 3\), candidates were not expected to use the second derivative but to show that the function decreases for \(x < 3\) and increases for \(x > 3\). Part (d) required a sketch which could have either been done on lined paper or on graph paper. The majority of candidates obtained at least two marks here with the most common errors seen being incomplete labelled axes and curves which were far from being smooth. In part (e), many candidates identified the correct coordinates for the two marks available. But for many candidates, this is where responses stopped as, in part (f), connecting the gradient function found in part (b) to the given coordinates proved problematic and only a significant minority of candidates were able to arrive at the required answer of –24. Indeed, there were many NR (no responses) to this part and the final part of the question. As many candidates found part (f) difficult, even more candidates found getting beyond the gradient of L very difficult indeed. A minority of candidates wrote down the gradient of their perpendicular but then did not seem to know where to proceed from there. Substituting their gradient for b and the coordinates (2, –12) into the equation \(x + by + c = 0\) was a popular, but erroneous, method. It was a rare event indeed to see a script with a correct answer for this part of the question.

