| Date | May 2015 | Marks available | 4 | Reference code | 15M.2.sl.TZ1.5 |
| Level | SL only | Paper | 2 | Time zone | TZ1 |
| Command term | Sketch | Question number | 5 | Adapted from | N/A |
Question
Consider the function \(f(x) = \frac{{96}}{{{x^2}}} + kx\), where \(k\) is a constant and \(x \ne 0\).
Write down \(f'(x)\).
The graph of \(y = f(x)\) has a local minimum point at \(x = 4\).
Show that \(k = 3\).
The graph of \(y = f(x)\) has a local minimum point at \(x = 4\).
Find \(f(2)\).
The graph of \(y = f(x)\) has a local minimum point at \(x = 4\).
Find \(f'(2)\)
The graph of \(y = f(x)\) has a local minimum point at \(x = 4\).
Find the equation of the normal to the graph of \(y = f(x)\) at the point where \(x = 2\).
Give your answer in the form \(ax + by + d = 0\) where \(a,{\text{ }}b,{\text{ }}d \in \mathbb{Z}\).
The graph of \(y = f(x)\) has a local minimum point at \(x = 4\).
Sketch the graph of \(y = f(x)\), for \( - 5 \leqslant x \leqslant 10\) and \( - 10 \leqslant y \leqslant 100\).
The graph of \(y = f(x)\) has a local minimum point at \(x = 4\).
Write down the coordinates of the point where the graph of \(y = f(x)\) intersects the \(x\)-axis.
The graph of \(y = f(x)\) has a local minimum point at \(x = 4\).
State the values of \(x\) for which \(f(x)\) is decreasing.
Markscheme
\(\frac{{ - 192}}{{{x^3}}} + k\) (A1)(A1)(A1)
Note: Award (A1) for \(-192\), (A1) for \({x^{ - 3}}\), (A1) for \(k\) (only).
at local minimum \(f'(x) = 0\) (M1)
Note: Award (M1) for seeing \(f'(x) = 0\) (may be implicit in their working).
\(\frac{{ - 192}}{{{4^3}}} + k = 0\) (A1)
\(k = 3\) (AG)
Note: Award (A1) for substituting \(x = 4\) in their \(f'(x) = 0\), provided it leads to \(k = 3\). The conclusion \(k = 3\) must be seen for the (A1) to be awarded.
\(\frac{{96}}{{{2^2}}} + 3(2)\) (M1)
Note: Award (M1) for substituting \(x = 2\) and \(k = 3\) in \(f(x)\).
\( = 30\) (A1)(G2)
\(\frac{{ - 192}}{{{2^3}}} + 3\) (M1)
Note: Award (M1) for substituting \(x = 2\) and \(k = 3\) in their \(f'(x)\).
\( = - 21\) (A1)(ft)(G2)
Note: Follow through from part (a).
\(y - 30 = \frac{1}{{21}}(x - 2)\) (A1)(ft)(M1)
Notes: Award (A1)(ft) for their \(\frac{1}{{21}}\) seen, (M1) for the correct substitution of their point and their normal gradient in equation of a line.
Follow through from part (c) and part (d).
OR
gradient of normal \( = \frac{1}{{21}}\) (A1)(ft)
\(30 = \frac{1}{{21}} \times 2 + c\) (M1)
\(c = 29\frac{{19}}{{21}}\)
\(y = \frac{1}{{21}}x + 29\frac{{19}}{{21}}\;\;\;(y = 0.0476x + 29.904)\)
\(x - 21y + 628 = 0\) (A1)(ft)(G2)
Notes: Accept equivalent answers.
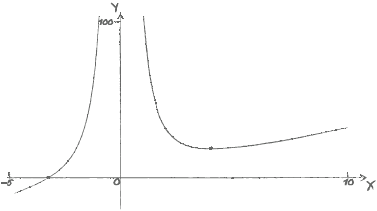 (A1)(A1)(A1)(A1)
(A1)(A1)(A1)(A1)
Notes: Award (A1) for correct window (at least one value, other than zero, labelled on each axis), the axes must also be labelled; (A1) for a smooth curve with the correct shape (graph should not touch \(y\)-axis and should not curve away from the \(y\)-axis), on the given domain; (A1) for axis intercept in approximately the correct position (nearer \(-5\) than zero); (A1) for local minimum in approximately the correct position (first quadrant, nearer the \(y\)-axis than \(x = 10\)).
If there is no scale, award a maximum of (A0)(A1)(A0)(A1) – the final (A1) being awarded for the zero and local minimum in approximately correct positions relative to each other.
\(( - 3.17,{\text{ }}0)\;\;\;\left( {( - 3.17480 \ldots ,{\text{ 0)}}} \right)\) (G1)(G1)
Notes: If parentheses are omitted award (G0)(G1)(ft).
Accept \(x = - 3.17,{\text{ }}y = 0\). Award (G1) for \(-3.17\) seen.
\(0 < x \leqslant 4{\text{ or }}0 < x < 4\) (A1)(A1)
Notes: Award (A1) for correct end points of interval, (A1) for correct notation (note: lower inequality must be strict).
Award a maximum of (A1)(A0) if \(y\) or \(f(x)\) used in place of \(x\).
Examiners report
Differentiation of terms including negative indices remains a testing process; it will continue to be tested. There was, however, a noticeable improvement in responses compared to previous years. The parameter k was problematic for a number of candidates.
In part (b), the manipulation of the derivative to find the local minimum point caused difficulties for all but the most able; note that a GDC approach is not accepted in such questions and that candidates are expected to be able to apply the theory of the calculus as appropriate. Further, once a parameter is given, candidates are expected to use this value in subsequent parts.
Parts (c) and (d) were accessible and all but the weakest candidates scored well.
Parts (c) and (d) were accessible and all but the weakest candidates scored well.
Part (e) discriminated at the highest level; the gradient of the normal often was not used, the form of the answer not given correctly.
Curve sketching is a skill that most candidates find very difficult; axes must be labelled and some indication of the window must be present; care must be taken with the domain and the range; any asymptotic behaviour must be indicated. It was very rare to see sketches that attained full marks, yet this should be a skill that all can attain. There were many no attempts seen, yet some of these had correct answers to part (g).
Curve sketching is a skill that most candidates find very difficult; axes must be labelled and some indication of the window must be present; care must be taken with the domain and the range; any asymptotic behaviour must be indicated. It was very rare to see sketches that attained full marks, yet this should be a skill that all can attain. There were many no attempts seen, yet some of these had correct answers to part (g).
Part (h) was not well attempted in the main; decreasing (and increasing) functions is a testing concept for the majority.

